CV Lecture 1

paolo

4 weeks

5个话题 ML

Introduction

What is CV

• enable machines to see

• Seeing implies more than taking a photograph or a video clip of the external world

• Light passes through the cornea(the clear front layer of the eye)The cornea bends light to help the eye focus
• Some of this light enters the eye through an opening called the pupil
• The iris(the coloured part of the eye) controls how much light the pupil lets in
• Next, light passes through the lens(a clear inner part of the eye). The lens works together with the cornea to focus light correctly on the retina.
• When light hits the retina(a light-sensitive layer of tissue at the back of the eye), special cells called photoreceptors turn the light into electrical signal.

Image Processing versus Computer Vision (the difference)

• Image Processing: generally, the enhancement, restoration, representation or transformation of visual data to aid in viewing and interpretation by humans.
• Computer Vision: automatic interpretation of visual data using computers(without humanintervention)

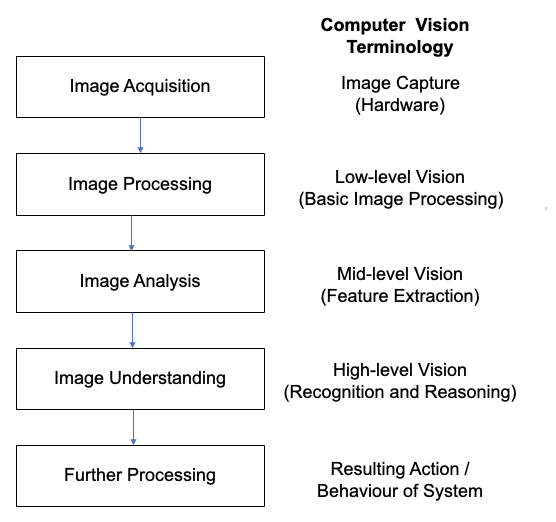
Typical computer Vision Processing Pipeline

What’s an image

•We mentioned the three colour channels in an earlier slide

•A colour image usually contains targets (objects, animals and/or people) that have distinctive characteristics, in computer vision called features

•Features could be delimiting edges, or points of interest

•Features could also be the textures of a fabric or skin or other making an object different from others

•Our first task is to find ways to implement algorithms that can detect these distinctive features to be able and identify targets and then describe them

Challenges in computer vision

• Ambiguity
  • Many different 3D scenes could have given rise to a particular 2D picture
• Complexity of a scence
  • Illumination
  • Object pose Clutter
  • Occlusions
  • Intra-class appearance
  • Viewpoint
• Scale of targets
• Dynamics
• Occlusion and clutter
• Intra-class variations

The importance of edges in and image

• use of outlines or edges of objects for:
  • recognition
  • perception of distance and orientation
• One of the most important aspects of human vision
  • visual cortex feature detectors that are tuned to the edges and segments of various widths and orientations

Edge based Segmentation

• Segmenting scene objects by discontinuity
  • image features where there is an abrupt change in intensity
  • indicating the end of one region and the beginning of another

How can we implement an edge detector

• Edge detection = differential operators to detect gradients of the gray or colour levels in the image
• If the image is I(x, y) then the basic idea is to compute

\[\]

Edge Detection Techniques

Image gradient

• Let the image be thus with partial derivatives we have:

\[\frac{\partial}{\partial x}f(x,y)=\frac{f(x+h,y)-f(x,y)}{h}\]

and \(\frac{\partial}{\partial y}f(x,y)=\frac{f(x,y+h)-f(x,y)}{h}\)

• An image $I(x,y)$ is digital object with discrete elements (picture elements, also called pixels)
• We can replace the partial derivatives with differences
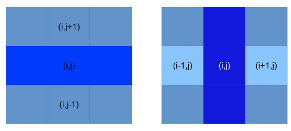
  • $\Delta_xI_{i,j}=I_{i+1,j}-I_{i,j}$
  • $\Delta_yI_{i,j}=I_{i+1,j}-I_{i,j}$
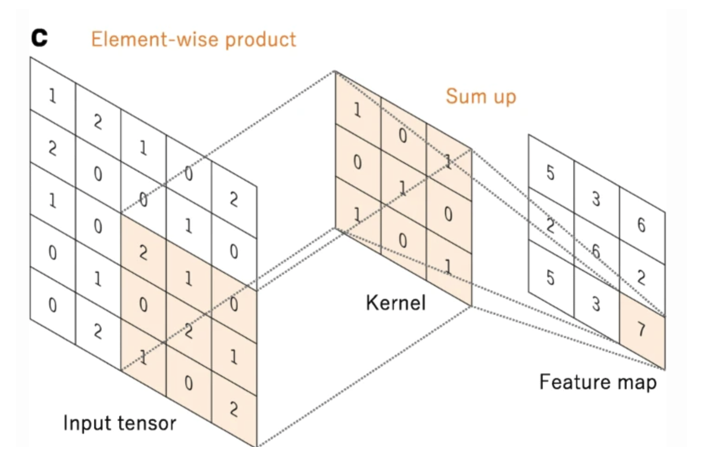
• These operations are equivalent to convolving $I_{i,j}$ with the digital function(-1, 1) in the x direction to calculate $\Delta_xI_{i,j}$ and $I_{i,j}$ with (-1,1) in y direction to calculate $\Delta_yI_{i,j}$

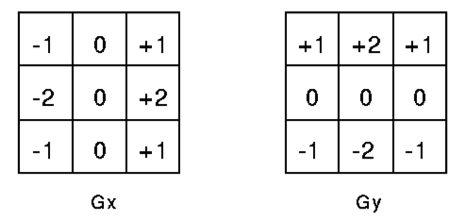
Sobel edge operator

• more computationally complex convolution masks(convolve image with both, both maskssum to zero)

• edge gradient magnitude is given by \(|G|=\sqrt{Gx^2+Gy^2}\)

• edge orientation: \(\theta=\tan^{-1}(\frac{Gy}{Gx})\)

• designed to respond maximally to edges running vertically and horizontally

  • one kernal for each of the two perpendicular orientations

• combined to get magnitude at each pixel and display this:

\[|G|=\sqrt{Gx^2+Gy^2}\quad|G|=|Gx|+|Gy|\]

Conclusions of the Sobel detector

• Advantages
  • Fast basic edge detection
  • Simple to implement using arithmetic operations
  • Useful as a measure of localised image texture (i.e. structured pattern)
• Disadvantages
  • output is noisy
  • resulting edge width, strength varies
• Importance
  • forms the basis for advanced edge detection, shape detection and object detection

Gaussian filter

• The Gaussian function in 1D is \(G(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^2}{2\sigma^2}}\)

• In 2D \(G(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}\)

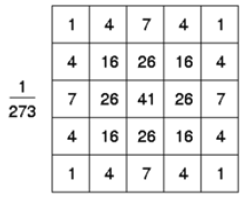
• We can use an approximation to generate a suitable kernel, the one below is for sigmaequals to 1

• The operation for isotropic Gaussian can be separated in two 1D filters, one for x and theother for y

• The 1D operations result much quicker

[[2025-01-13-CV-2]]