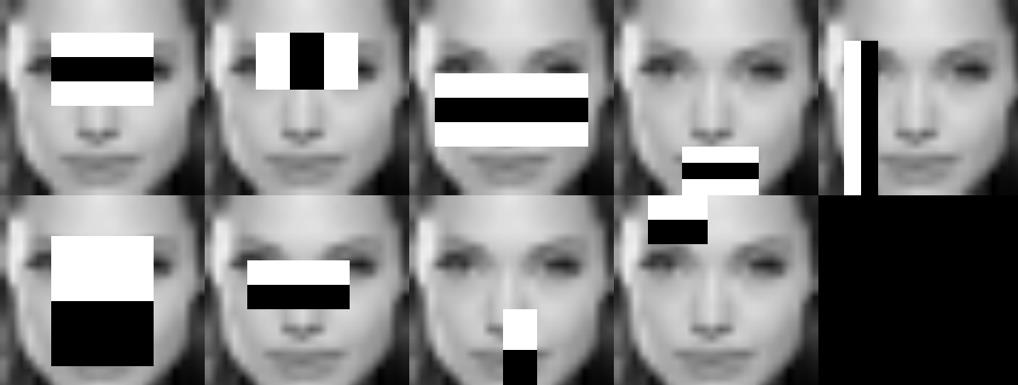DLVR 1 Deep Neural Networks

对于作业 常见错误 贴代码截图等

Deep Learning Computer Vision & Robotics Part I. Basic Deep Neural Networks

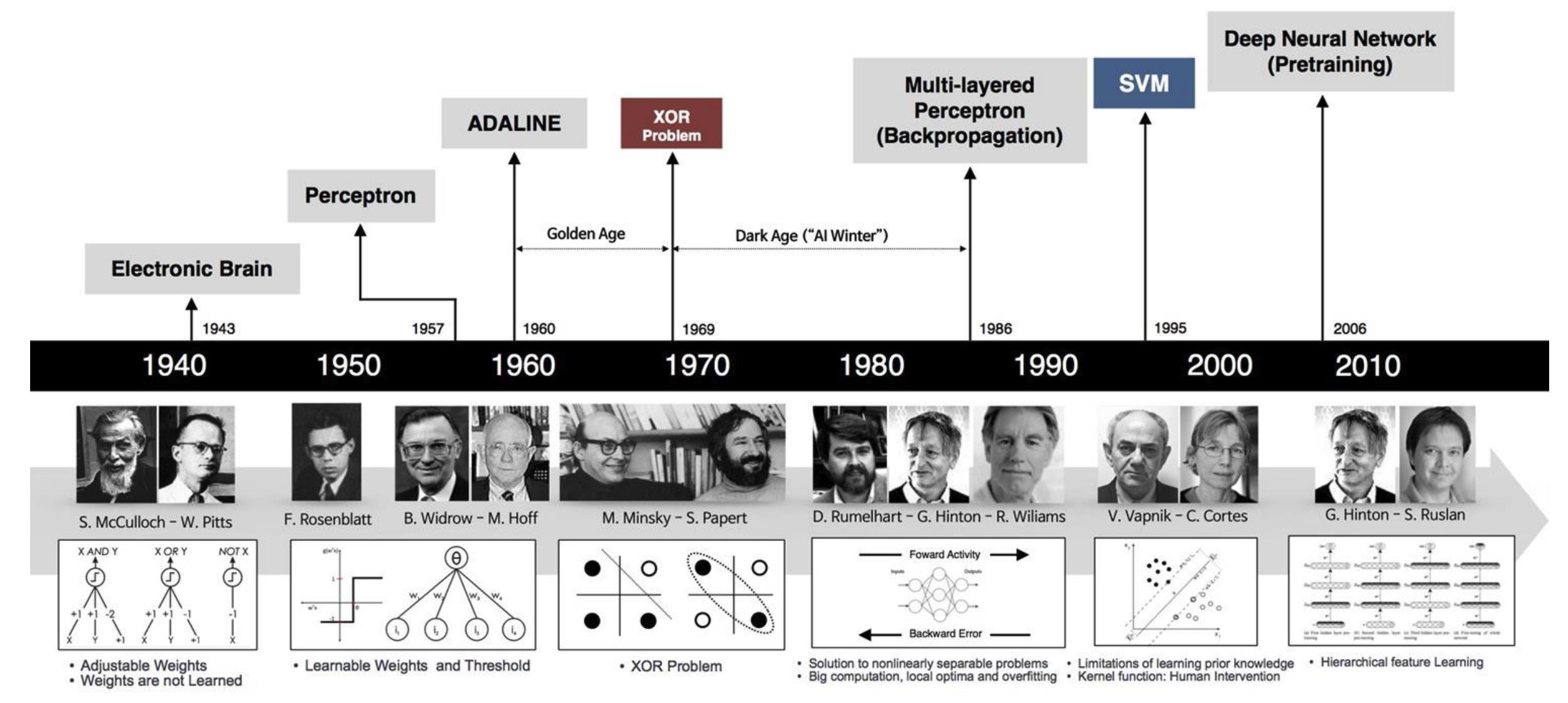
• 1980s - Rediscover Back-propagation
• 1990s - Winter for Neural Networks
  • LeNet Handwritten Digits Recognition
• 2000s - Era of Internet & Gaming
  • Massive Data & GPGPUs
• 2010s - Early Success & Boom of ANN
  • AlexNet (CNN) on ImageNet
  • LSTM & Transformers (Attention)
• 2024 - Nobel Prize Winners
  • Physics - Artificial Neural Networks
  • Chemistry - AlphaFold Protein Design

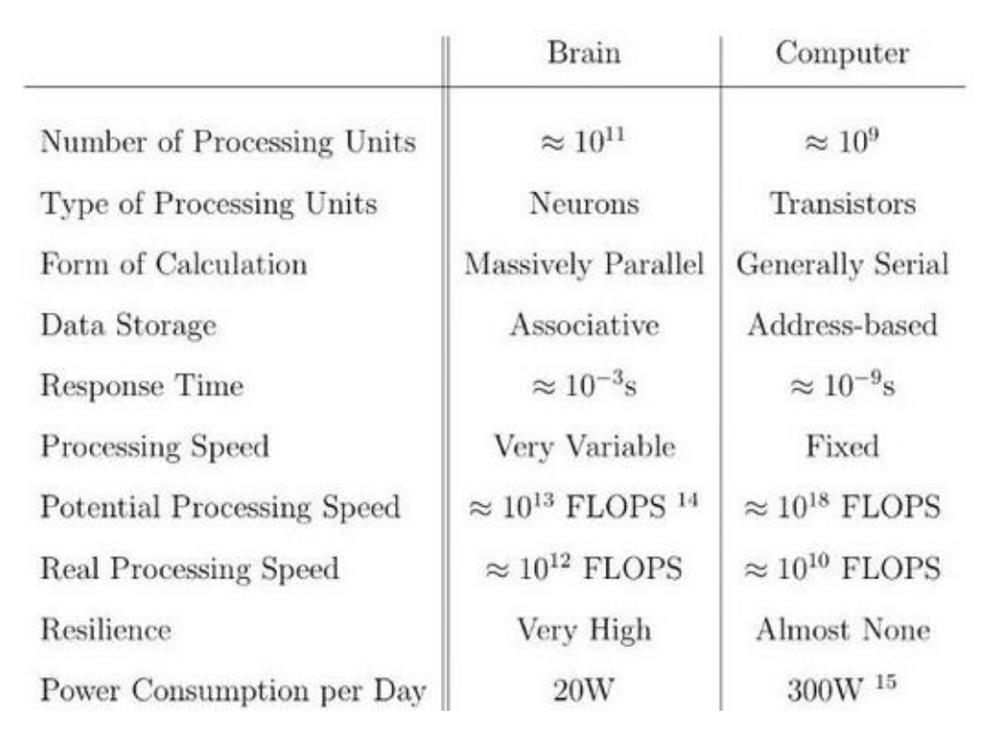
Background & History-Artificial Intelligence & Neural Networks

“Shallow” Learning Driven AI Era

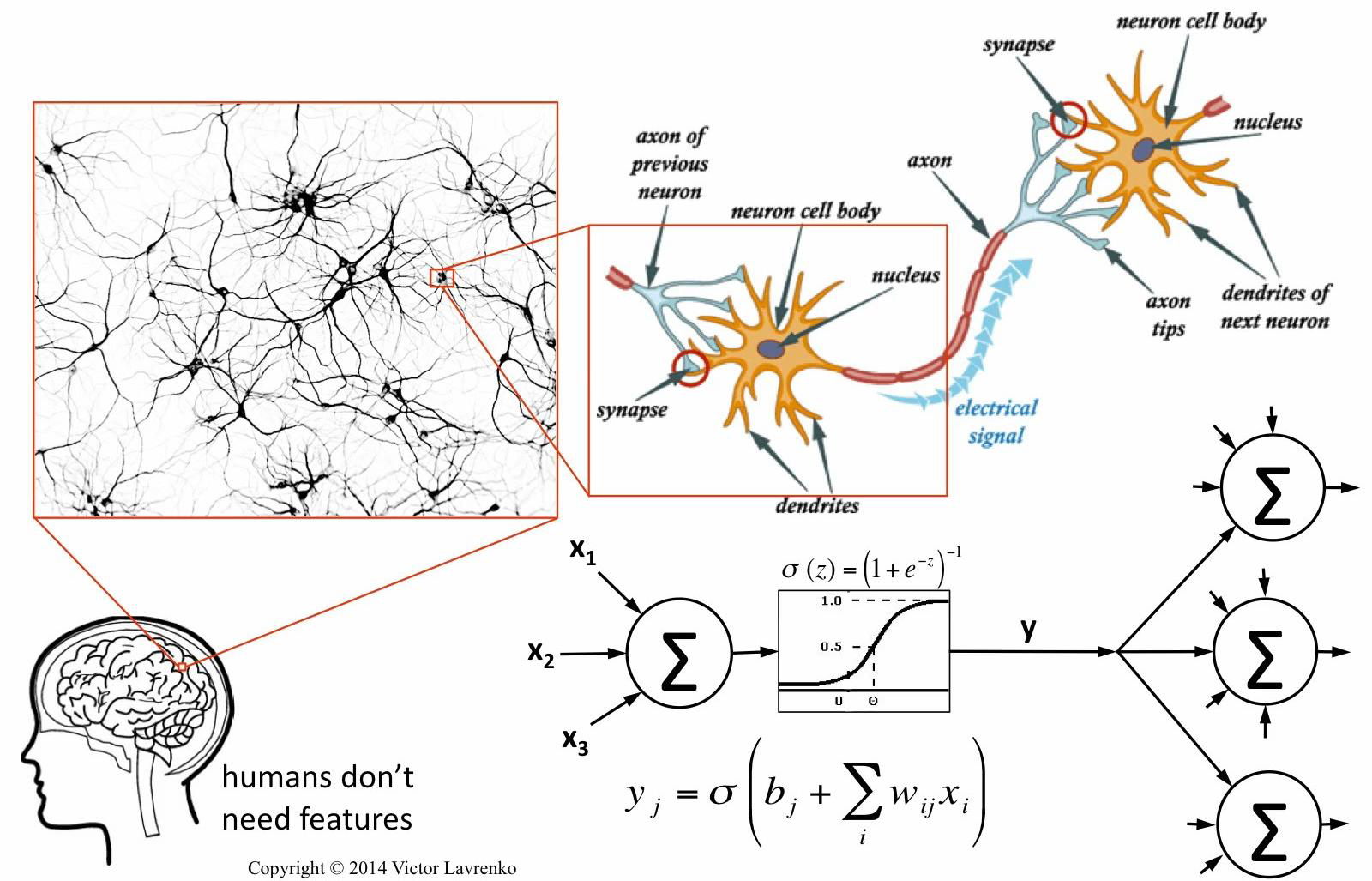
Computational Neuron Model (Neuroscience Inspired)

“Deep” Learning Driven AI Era

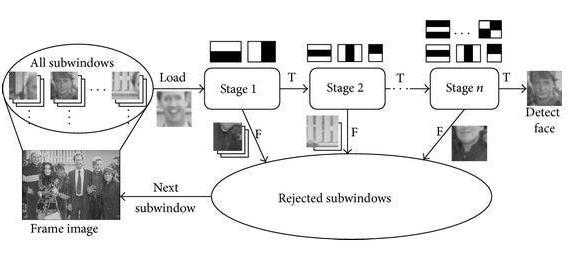
Face Detection: Classic Approach v.s. Deep Learning

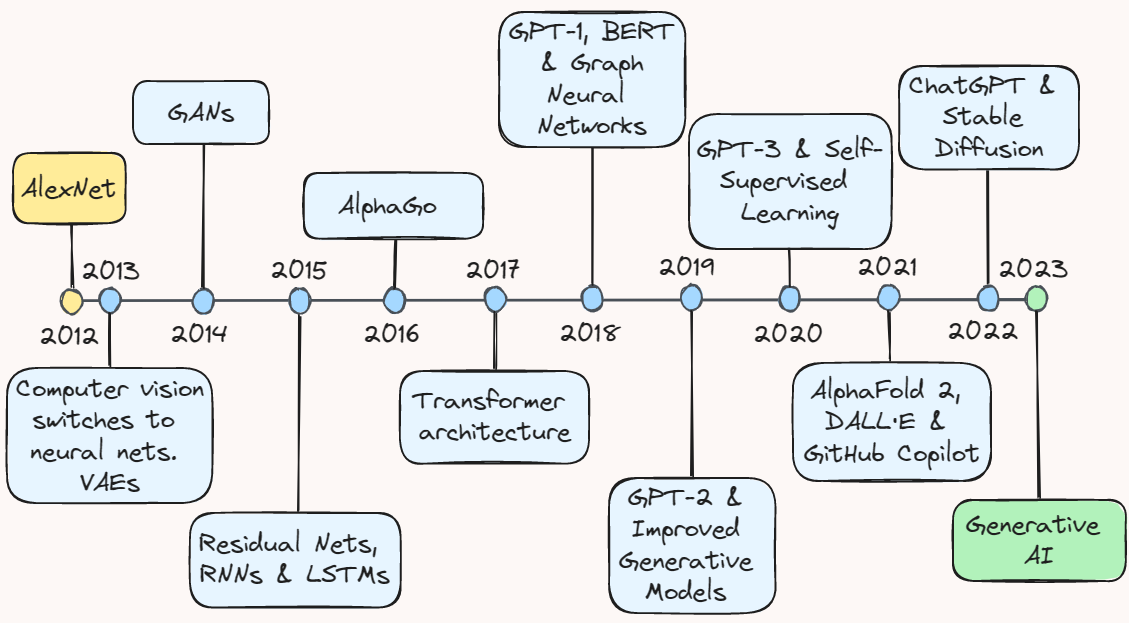
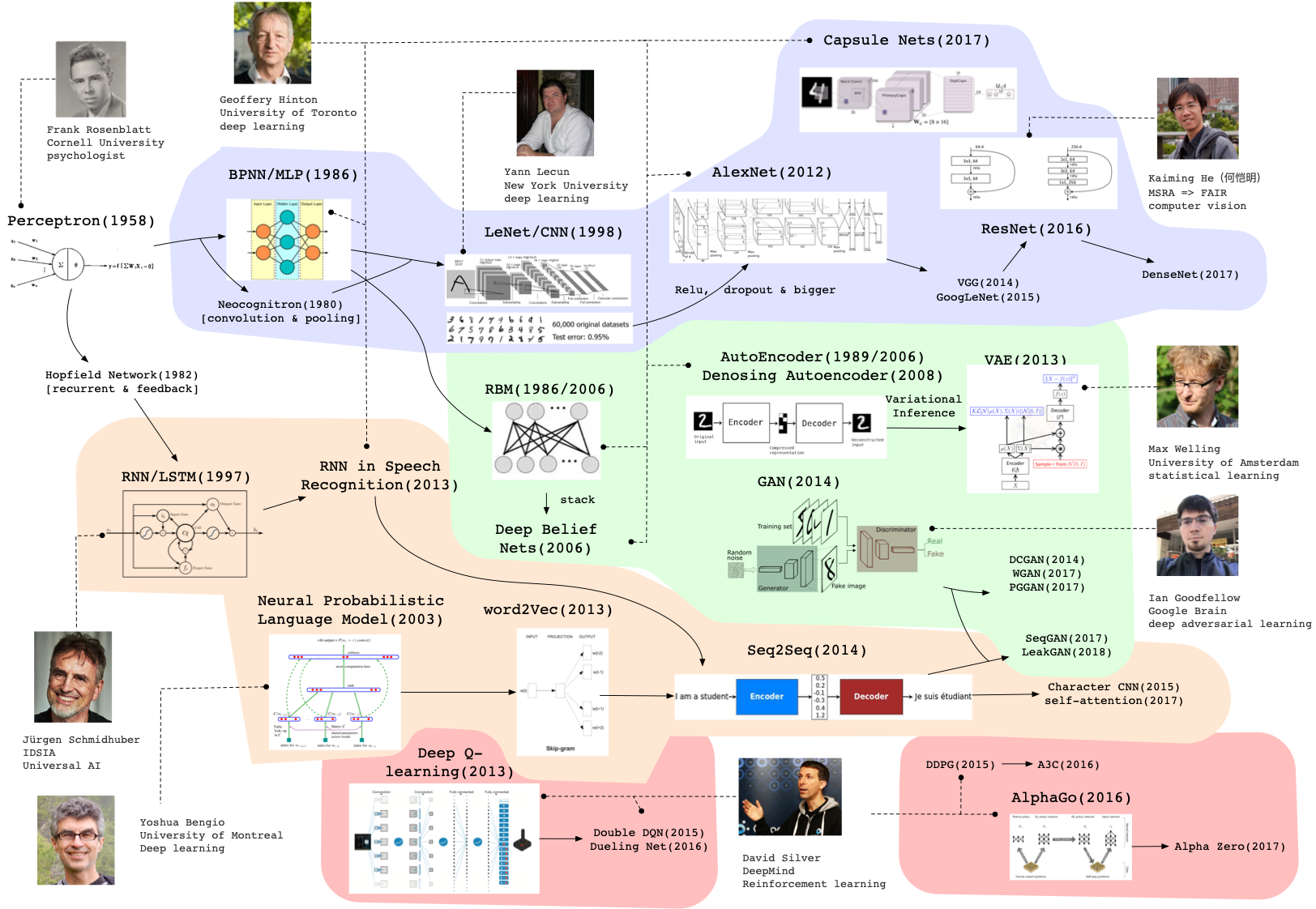
An Incomplete Map of Deep Learning Territory (Until 2023)

Start with “Shallow” NNs

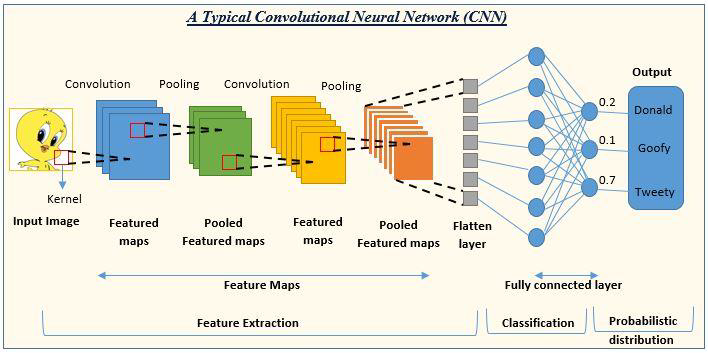
Basic Building Blocks for CNNs

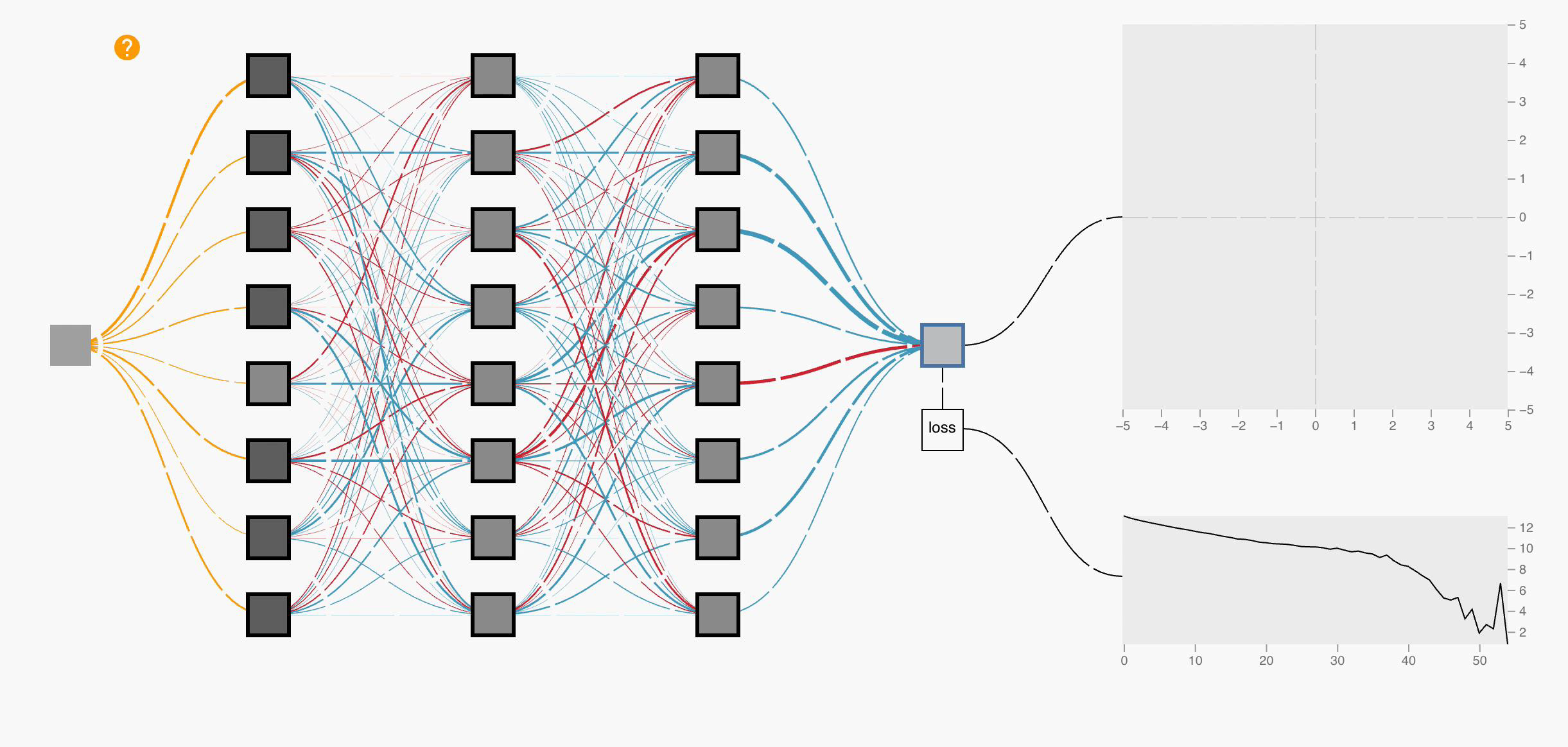
Example 1: Regression Artificial Neural Networks (ANNs)

This example uses the Boston Housing Dataset to predict the median value of owner-occupied homes (per 1000 dollars).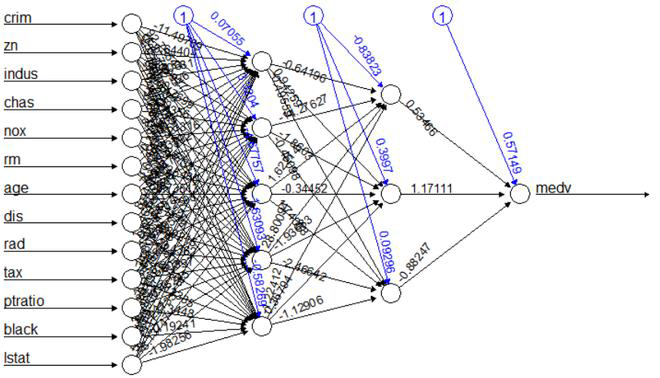

• crim per capita crime rate by town.
• zn proportion of residential land zoned for lots over 25,000 sq.ft.
• indus proportion of non-retail business acres per town.
• chas Charles River dummy variable (= 1 if tract bounds river; 0 otherwise).
• nox nitrogen oxides concentration (parts per 10 million).
• rm average number of rooms per dwelling.
• age proportion of owner-occupied units built prior to 1940.
• dis weighted mean of distances to five Boston employment centres.
• rad index of accessibility to radial highways.
• tax full-value property-tax rate per $10,000.
• ptratio pupil-teacher ratio by town.
• black 1000(Bk - 0.63)² where Bk is the proportion of blacks by town.
• lstat lower status of the population (percent).
• medv median value of owner-occupied homes in $1000s.

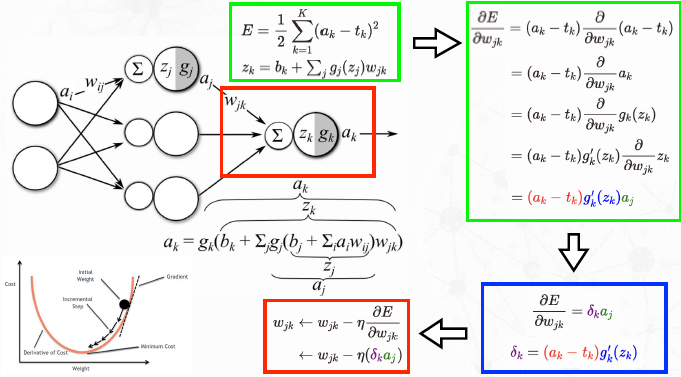
Recap - A Simple Neural Network Model

• $z_j$: input to node $j$ in layer $l$
• $g_j$: activation function for node $j$ in layer $l$ (applied to $z_j$)
• $a_j = g_j(z_j)$: the output/activation of node $j$ in layer $l$
• $b_j$: bias/offset for unit $j$ in layer $l$
• $w_{ij}$: weights connecting node $i$ in layer $(l - 1)$ to node $j$ in layer $l$
• $t_k$: target value for node $k$ in the output layer \(E = \frac{1}{2} \sum_{k=1}^{K}(a_k - t_k)^2\) Training Dataset

| # ID | X1 | Xn | $t_k$ | |——-|——-|——-|————-| | 00001 | ……| ……| …… | | 00002 | ……| ……| …… | | ……| ……| ……| …… | | 99999 | ……| ……| …… |

1. https://dustinstansbury.github.io/theclevermachine/derivation-backpropagation

The Output Layer - Gradient Descent

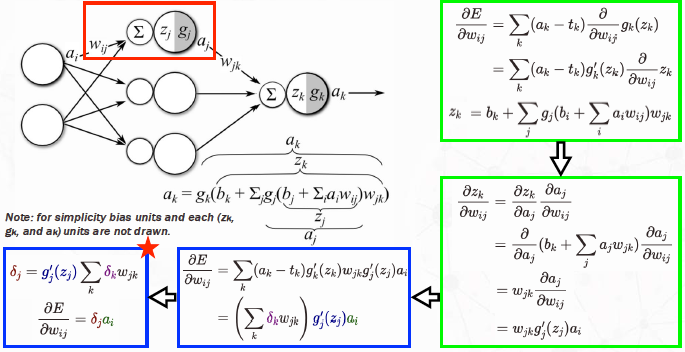
The Hidden Layer - Error Propagation

Back-Propagation

\(\delta_k = (a_k - t_k)g_k'(z_k) \rightarrow \frac{\partial E}{\partial w_{jk}} = \delta_k a_j\)

\[\delta_j = g_j'(z_j) \sum_k \delta_k w_{jk} \rightarrow \frac{\partial E}{\partial w_{ij}} = \delta_j a_i\]