IML L3.3 SVM

Support vector machine

Support vector machine are a popular Machine Learning tool.

• they can be used both for classification and regression
• they can be used for a linear and non-linear models

We will consider a binary classification problem with positive $y=+1$ and negative $y=−1$ classes.

Objective

The goal of a Support vector machine is to separate the two classes using a line that maximizes the minimal distance (margin) of the data to the decision boundary.

There are two types of large margin classification

• hard margin classification:
  • we do not tolerate any data points in the margin
  • only works on linearly separable data
  • sensitive to outliers (a single point can change the data from separable to non-separable)

• soft margin classification:
  • we tolerate a small amount of data in the margin region or even on the wrong side of the margin

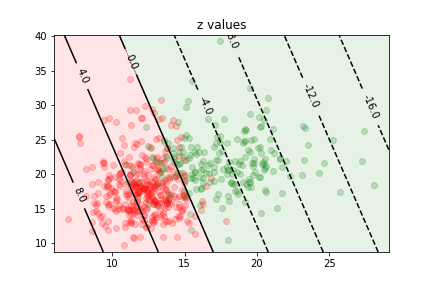
For our linear model the value

\(z = w_0 + \vec x \cdot \vec w\) is proportional to the distance to the z=0z=0 curve:

\(d = \frac{z}{||\vec w||}\)

By rescaling $\vec w$ we change the relationship between the distance and the value of $z$.

In a SMV we declare our margin to be between $z=1$ and $z=−1$ and find the value of $w_0$, $\vec w$ that

• minimizes the amount of data in the margin (margin violation)
• maximizes the width of the margin

The two goals are in conflict!

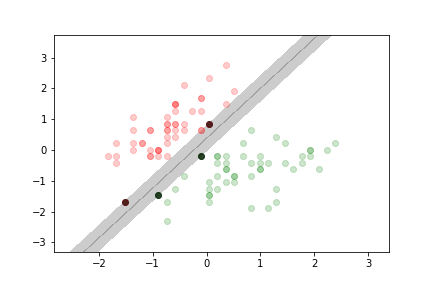
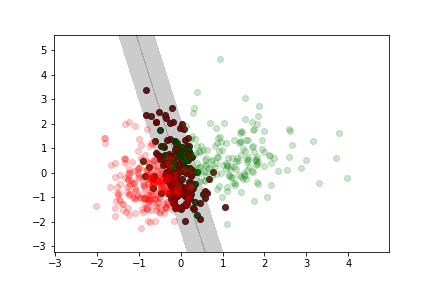
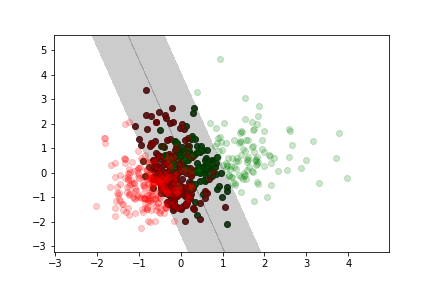
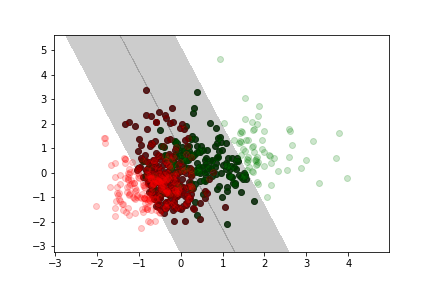
Example

Here we use the iris dataset again, but we rescaled the features so that they have 0 mean and unit standard deviation.

no margin violation

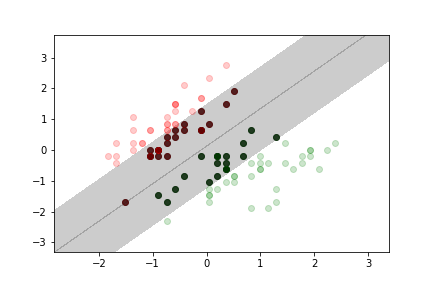
moderate margin violation

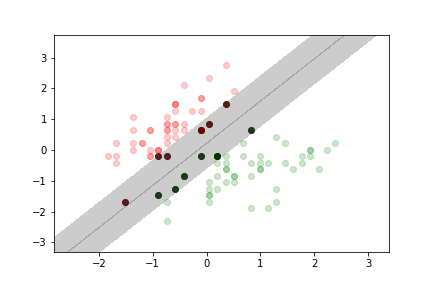
more margin violation

Non separable example

Here we use the cancer data set we used for previous lectures and exercises.

Less margin violation

Moderate margin violation

More margin violation

Training a SVM

Adding data to the training set only affects the model if the additional point falls into the margin.

The model is completely defined by the data samples at the boundary or inside the margin (this is where the name comes from, these data samples are the “support” vectors)

Note: Unlike in the logisitic regression case, there is no probabilistic interpretation for a SVM.