IML L1.2

Perceptron 感知器

Perceptron algorithm was the first “Machine learning” algorithm

• invented in 1957 by Frank Rosenblatt

Classification

We have a set of examples of items from two classes. We want to train a model to distinguish between the two classes for new items.

Notation

Training data is composed of $n_d$ samples, each of which has $n_f$ features. Each data sample’s class label is encoded as $\pm1$. \(\begin{array}{ccc}\text{features:}&\mathrm{x_{j}^{(i)},}&1\leq\mathrm{i}\leq\mathrm{n_{d},},&1\leq\mathrm{j}\leq\mathrm{n_{f}}\\\\\text{labels:}&\mathrm{y^{(i)}=\pm1,},&1\leq\mathrm{i}\leq\mathrm{n_{d}}\end{array}\)

Model

We will train a linear model \({z(x,w)=w_0+\sum_jx_jw_j }\) with $n_f + 1$ parameters \({w_{j},\quad0\leq j\leq n_{f}}\) We will use the decision function \(\phi(z)=\mathrm{sgn(z)}\) If $\phi(z)=+1$ our model predicts the object to belong to the first class, if ϕ(z)=−1ϕ(z)=−1 the model predicts that the object belongs to the second class.

Now we need to set the parameters wjwj such that our pediction is as accurate as possible.

–

Learning rate

The parameter ηη in the update rule $$

$$

\[\omega_0\rightarrow\omega_0+\eta y^{(i)}\]

is a parameter of the algorithm, not a parameter of the model or of the problem. It is an example or hyperparameter超参数 of a learning algorithm.

The learning rate set how much a single misclassification should affect our parameters.

• a too large learning rate will lead to the paramters “jumping” around their best values and give slow convergence
• a too small learning rate will make more continuous updates but it might take many epochs to get to the right values

Convergence 收敛

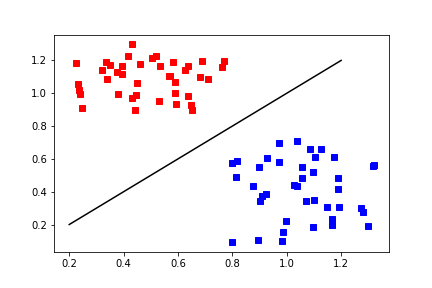
• The perceptron algorithm is converging if the classes are linearly separable in the training set. 如果类在训练集中是线性可分的，则感知器算法正在收敛。
• It might take a long time to converge(收敛)

Linearly separable 线性可分

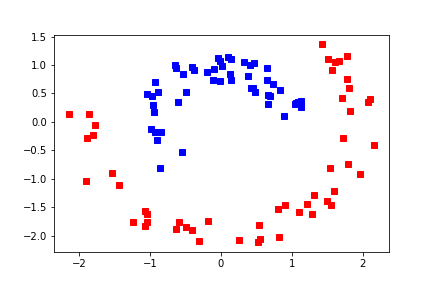
Separable, but not linearly 可分离，但不是线性的

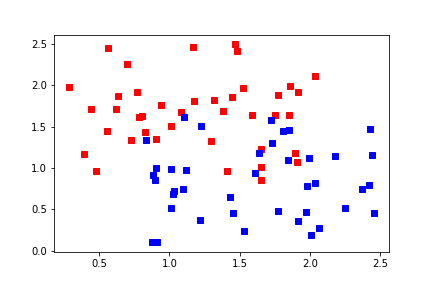
Probably not separable 可能无法分离

• Problems with the perceptron algorithm 感知器算法的问题

  • convergence depends on order of data 收敛取决于数据的顺序
    • random shuffles 随机洗牌
  • bad generalisation 不好的概括

Bad generalisation 不好的概括

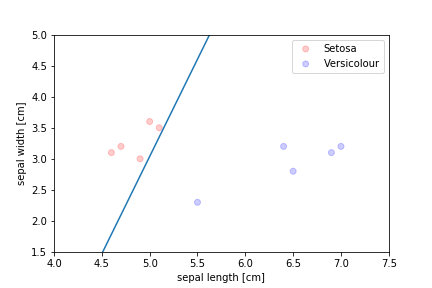
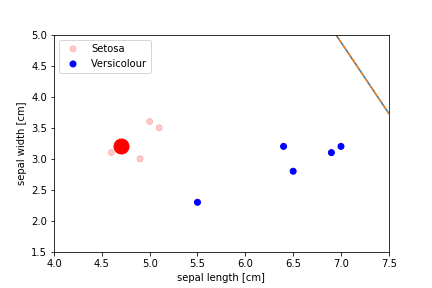
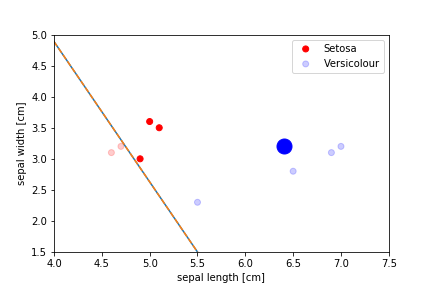
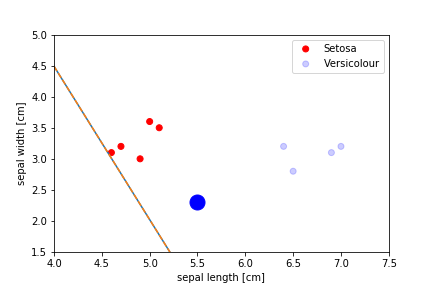
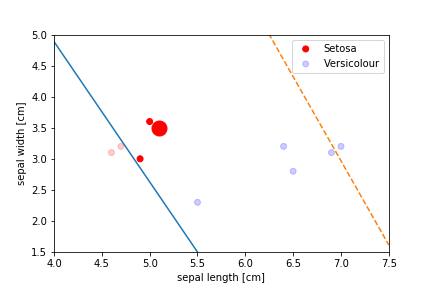
The algorithm stops when there is no errors left but often the demarcation line ends up very close to some of the instances, which leads to bad generalisation 当没有留下错误时，算法会停止，但分界线通常会非常接近某些实例，这会导致不良的泛化

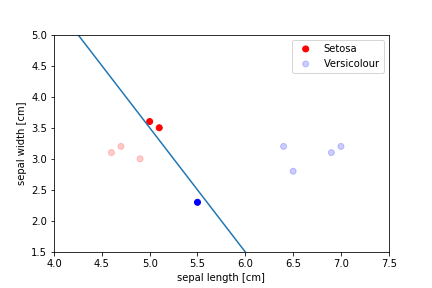
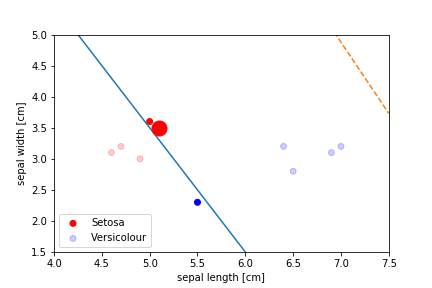
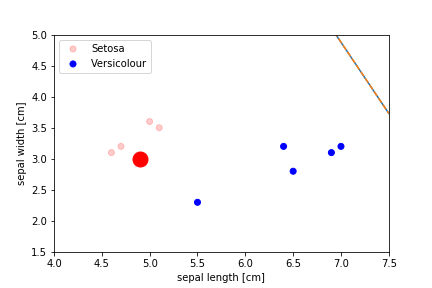
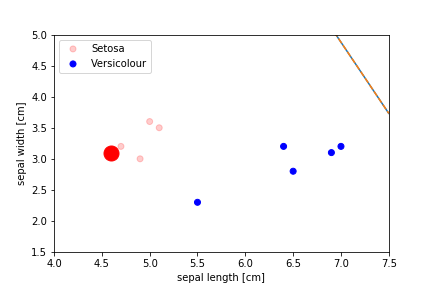
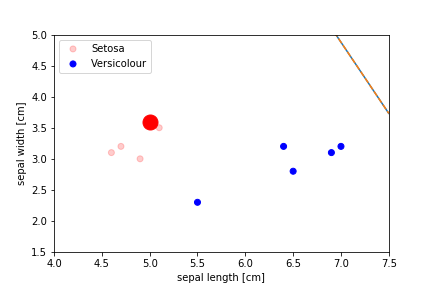
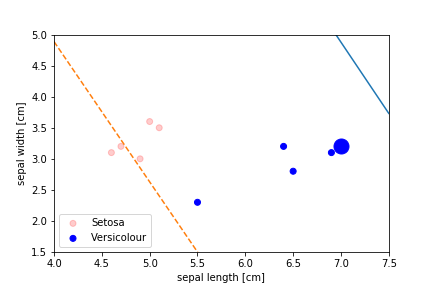
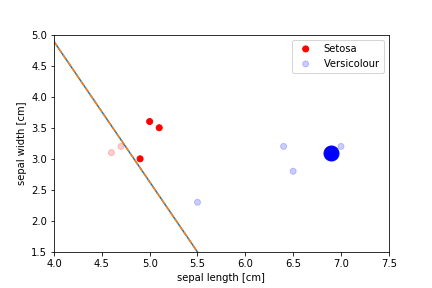
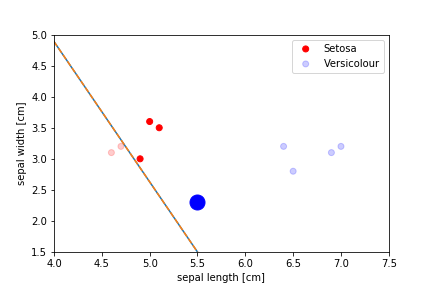
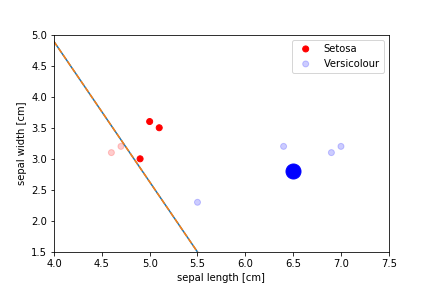
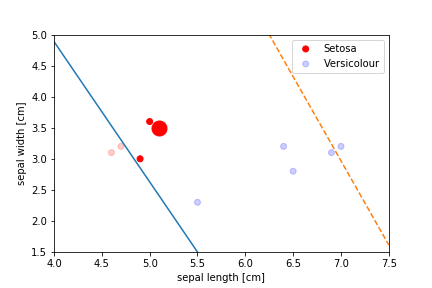
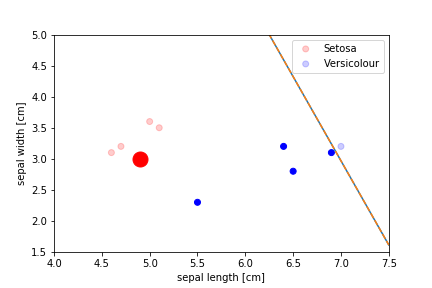
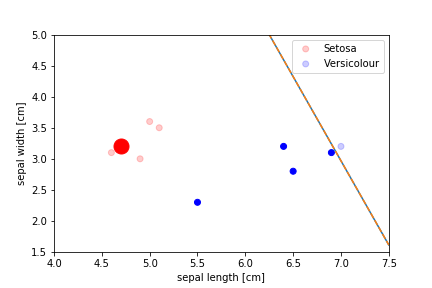
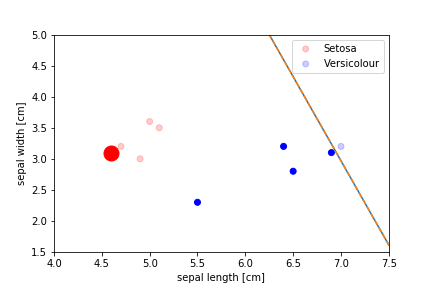
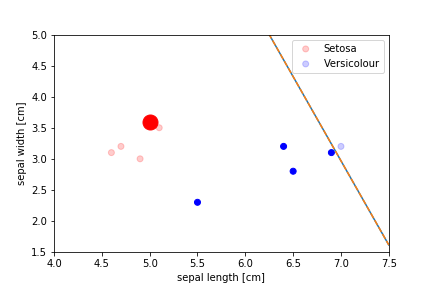
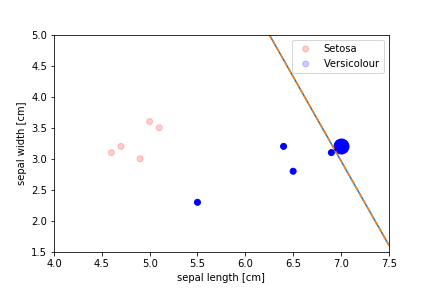
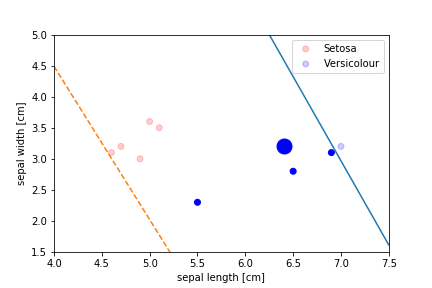
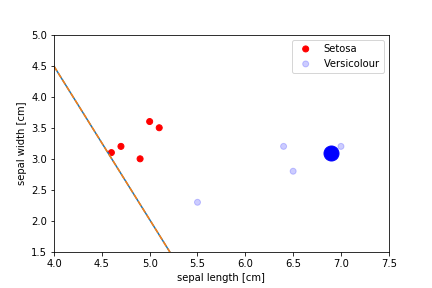
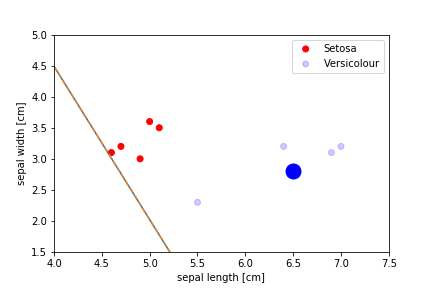
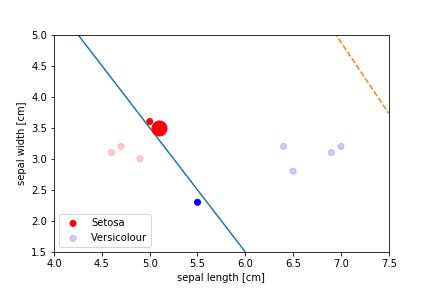
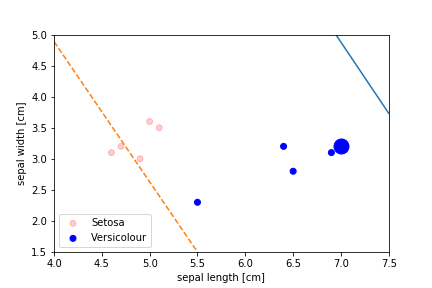
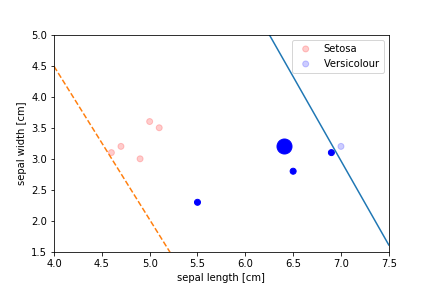
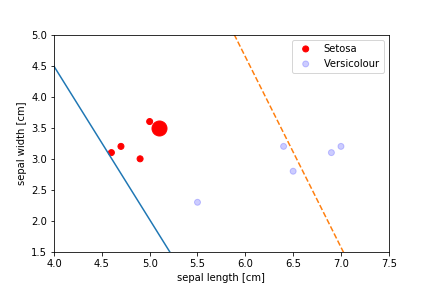
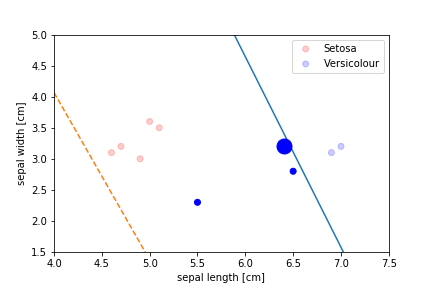
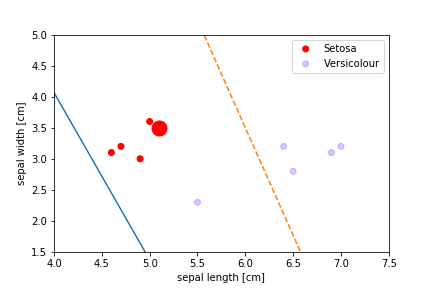
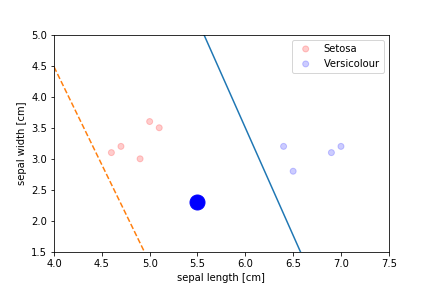
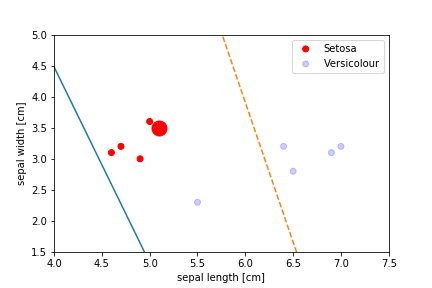
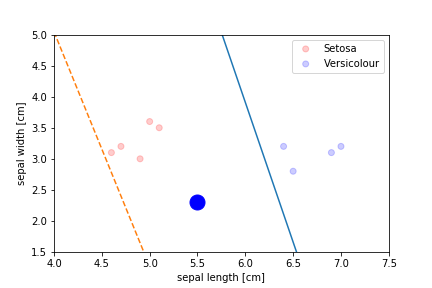
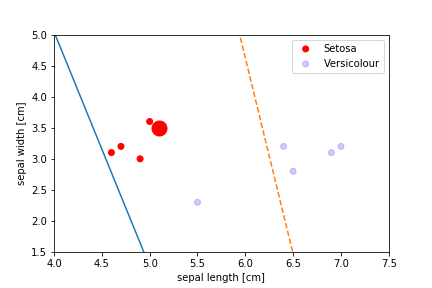
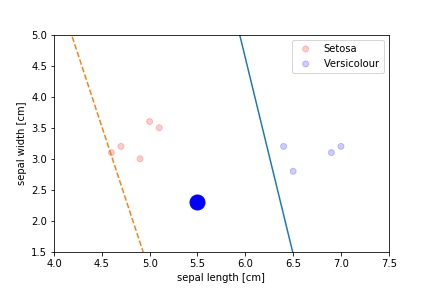
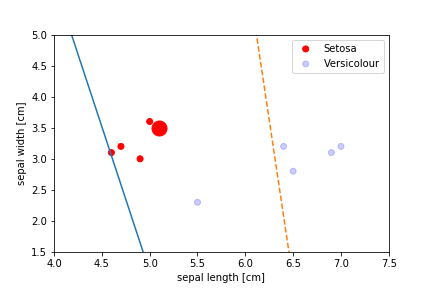
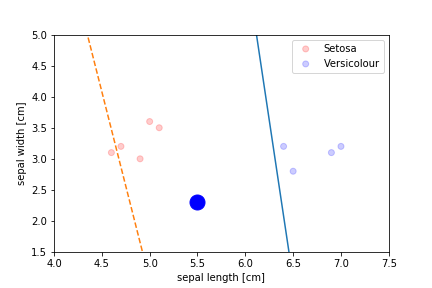
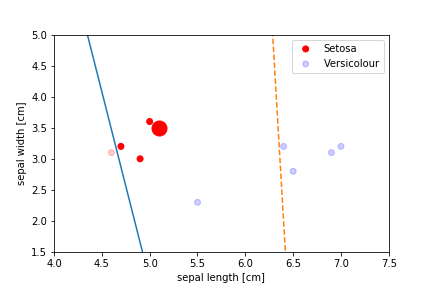
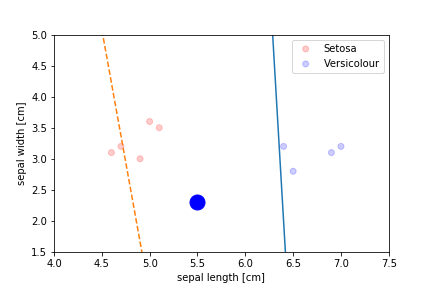
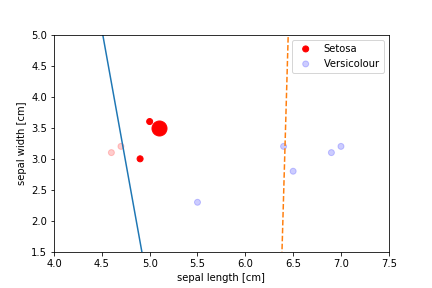
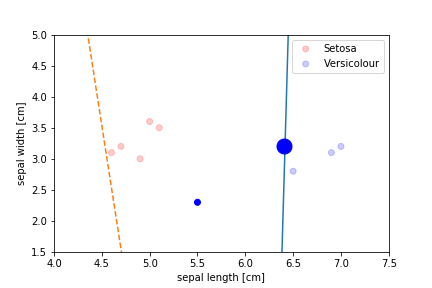
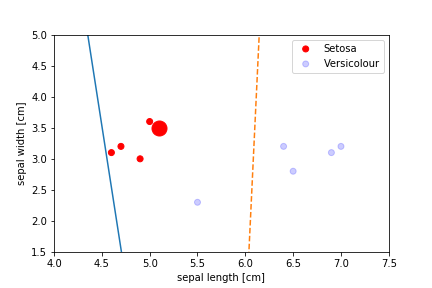
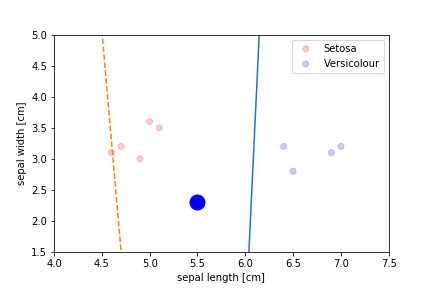
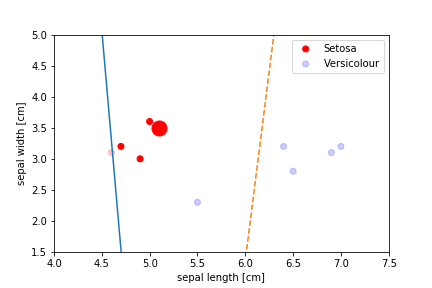
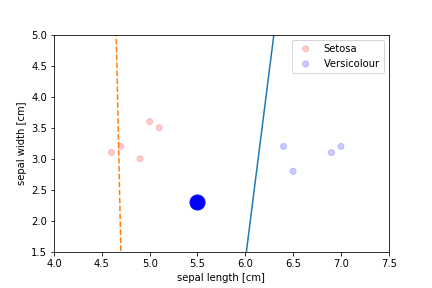
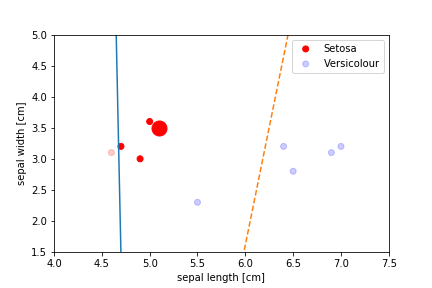
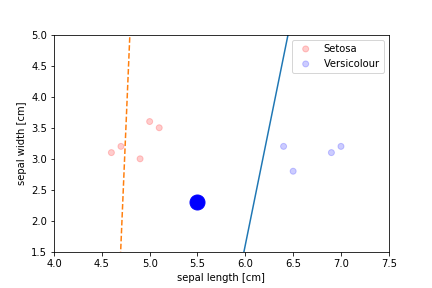
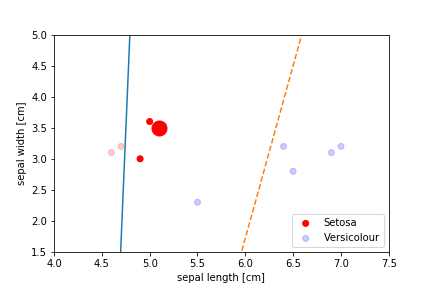
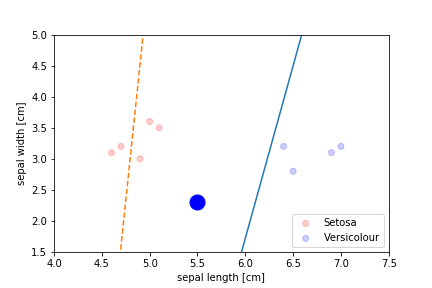
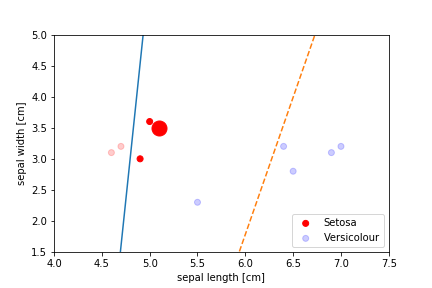
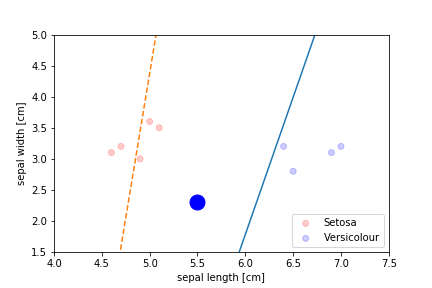
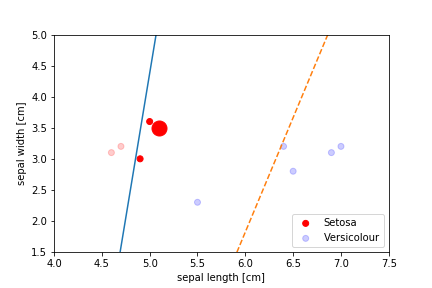
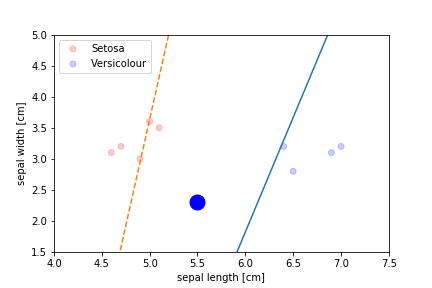
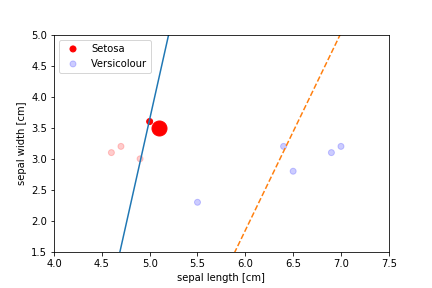
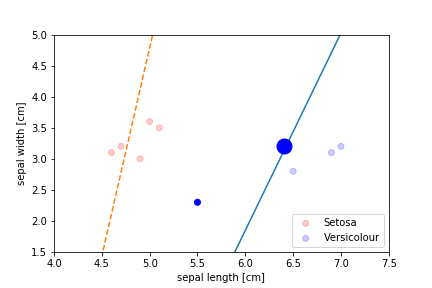
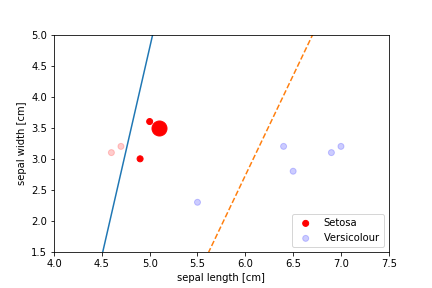
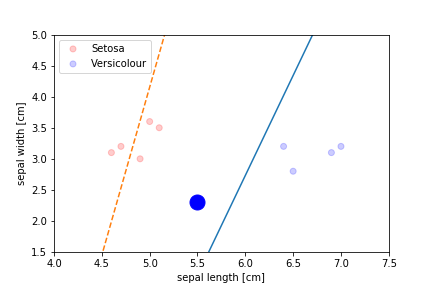
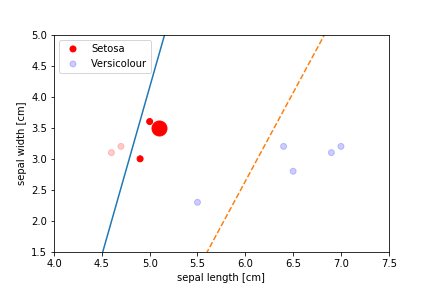
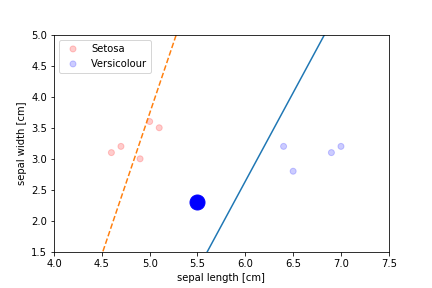
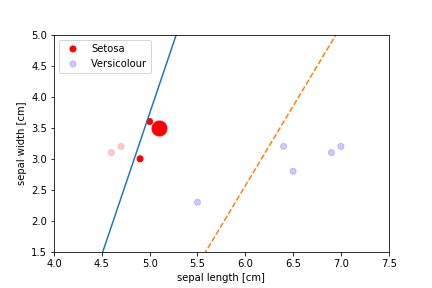
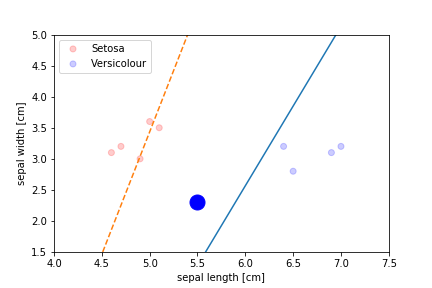
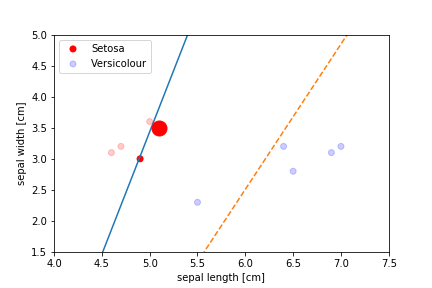
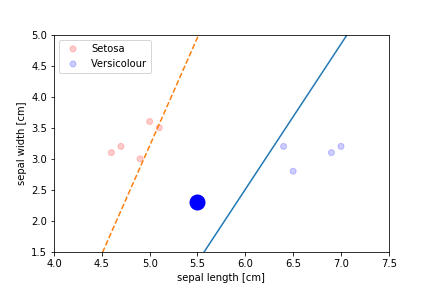
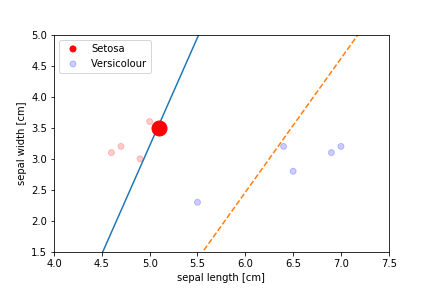
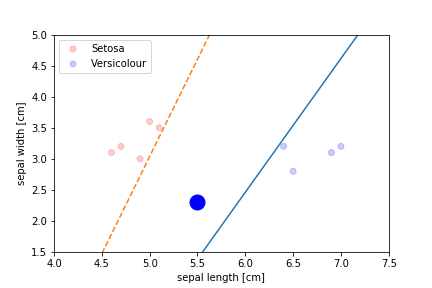
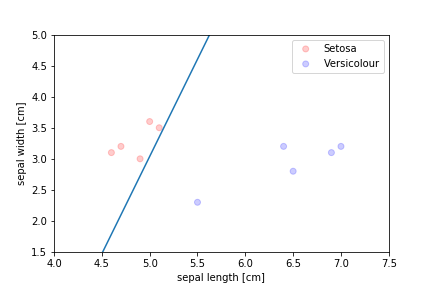
Perceptron Demo

initial position

First epoch

Second epoch

All epochs

Only show when the parameters change