PO Lecture 3 Roofline Models

PO Lecture 3 Roofline Models

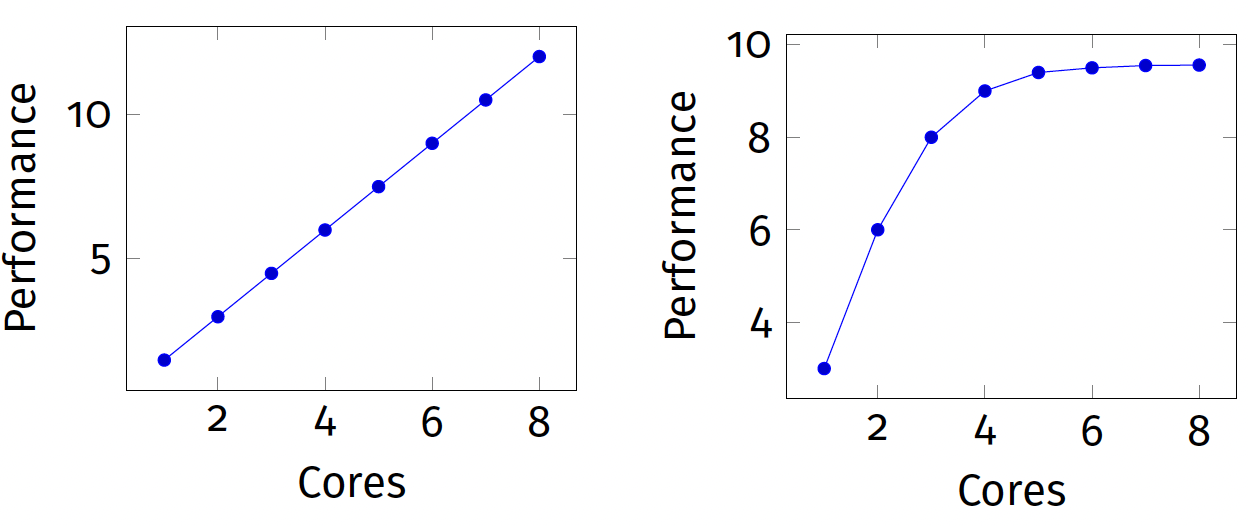
Exercise 2: results

—-wait

page4

–

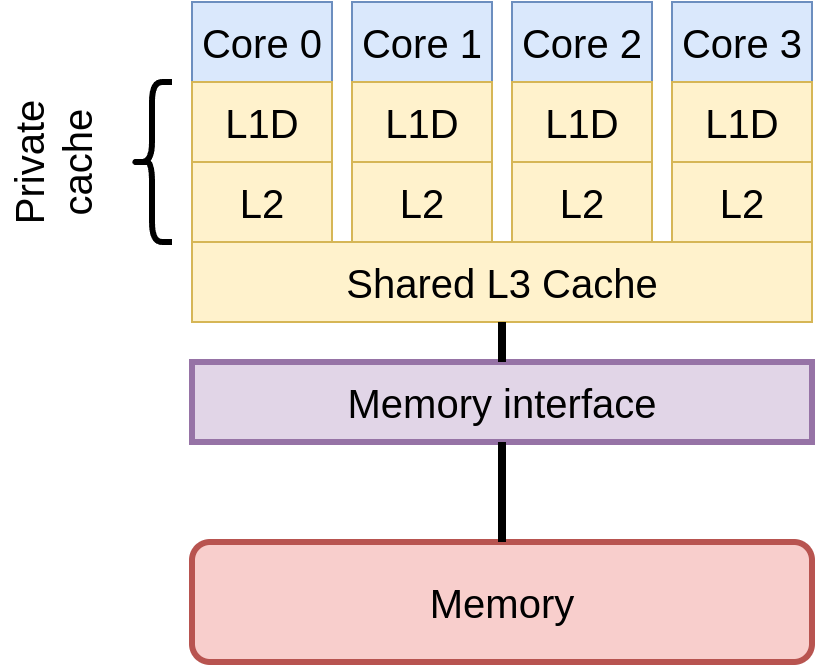
# Memory/node topology

likwid-topology reports an ASCII version of diagrams like this.

Exercise 3: results

Conclusions on hardware architecture

Performance considerations

• How many instructions are required
• How efficiently a processor can execute those instructions
• The runtime contribution of the data transfers

Complex “topology” of hardware

• Many layers of parallelism in modern hardware
• Sockets: around 1-4 CPUs on a typical motherboard
• Cores: around 4-32 cores in a typical CPU
• Vectorisation: 2-16 floats per vector registers
• Superscalar execution: typically 2-8 instructions per cycle

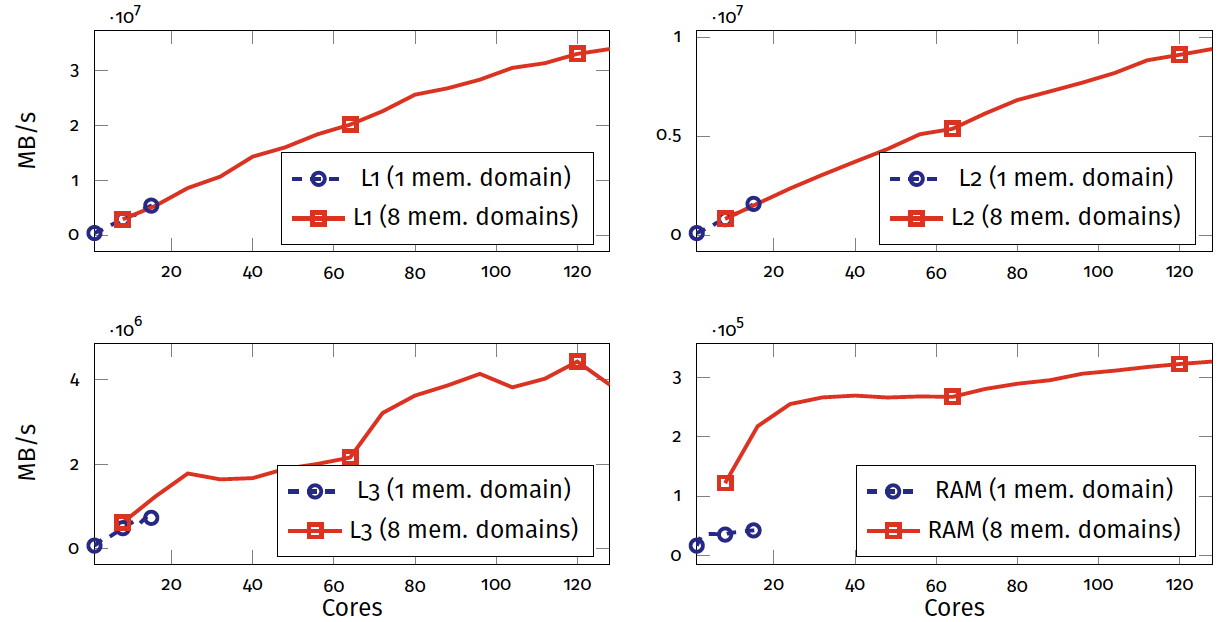
Types of resources

Scalable	Saturating
Scales linearly	Scales sublinearly
- private resources	- shared resources
- floating-point units	- L3 memory
- CPU cores	- RAM

Bottlenecks Saturating resources are the limiting factor.

Scalable vs. Saturating

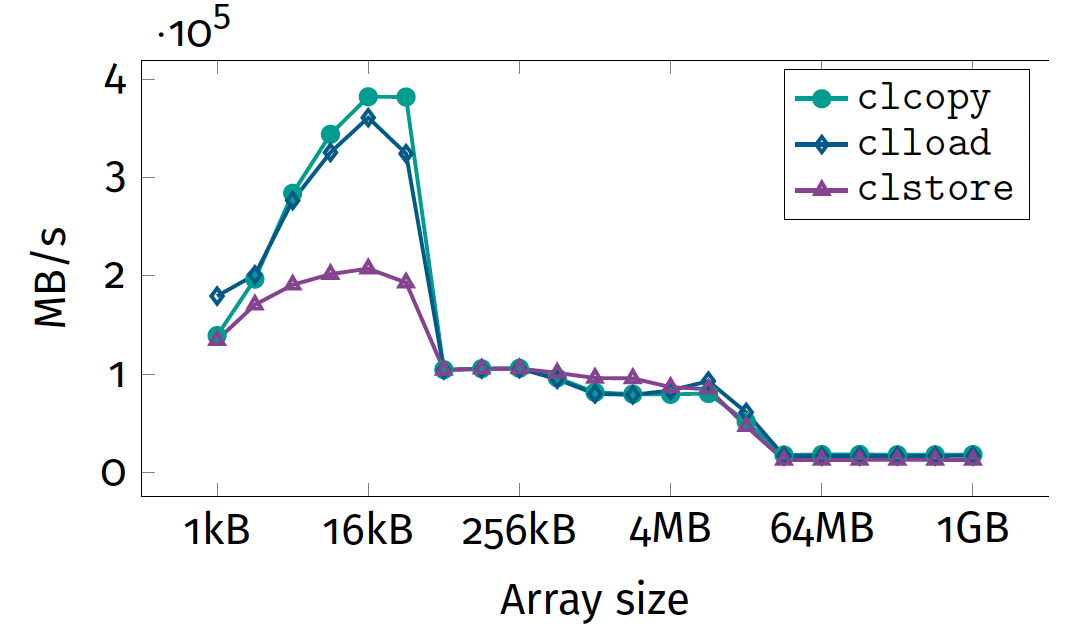
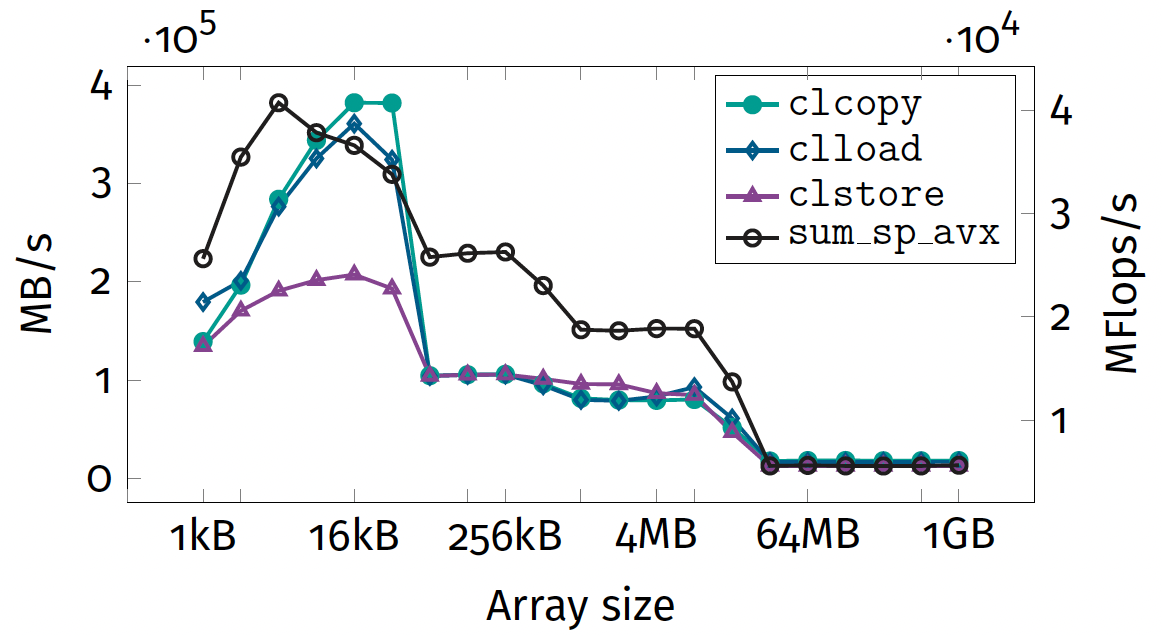
More realistic memory benchmark

The clcopy benchmark we used

• only touches one byte in each cache line
• only provides upper bounds
• is not a realistic workload

State-of-the-art alternative

• STREAM benchmark¹
• most commonly used is TRIAD
• available in likwid-bench as stream_triad_XXX

¹https://www.cs.virginia.edu/stream/

The TRIAD loop

double *a, *b, *c;
double alpha = 1;
...
for (int i = 0; i < N; i++)
    a[i] = b[i]*alpha + c[i];

• 2 floating point operations
• 2 loads

• 1 store

• ==compile -> alpha disappear why?==

Code optimisation

Simple model for loop heavy code

Simple view of hardware

Simple view of software

// Possibly nested loops  
for (i = 0; i < ...; i++)  
// Complicated code doing  
// M Flops causing  
// B bytes of data transfer  

Operational intensity [Flops/B] $I_c=\frac{M}{B}$

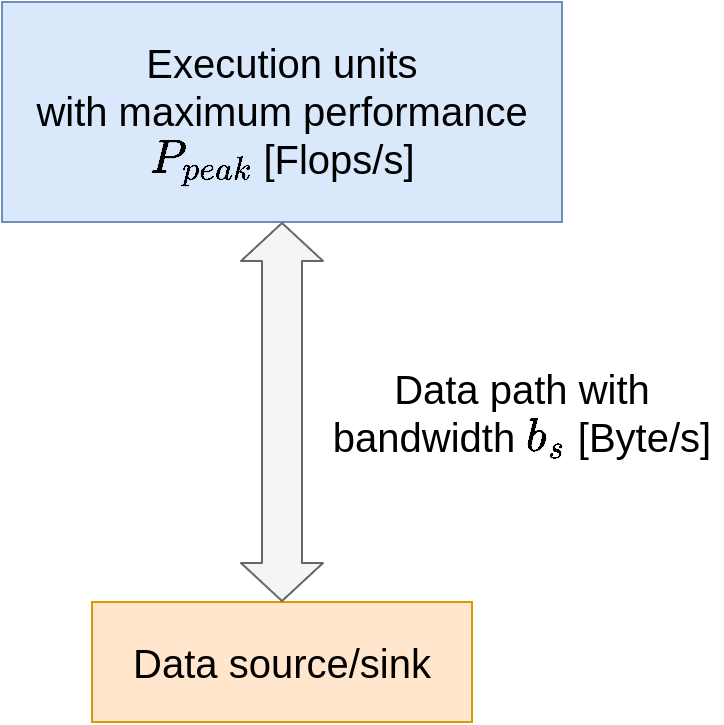
The roofline model

What is the performance P of a code? How fast can work be done? P measured in Flops/s

The bottleneck is either:

• execution of work P_peak
• or the data path I_c · b_s

Therefore: $P=min(P_{peak},I_c·b_s)$

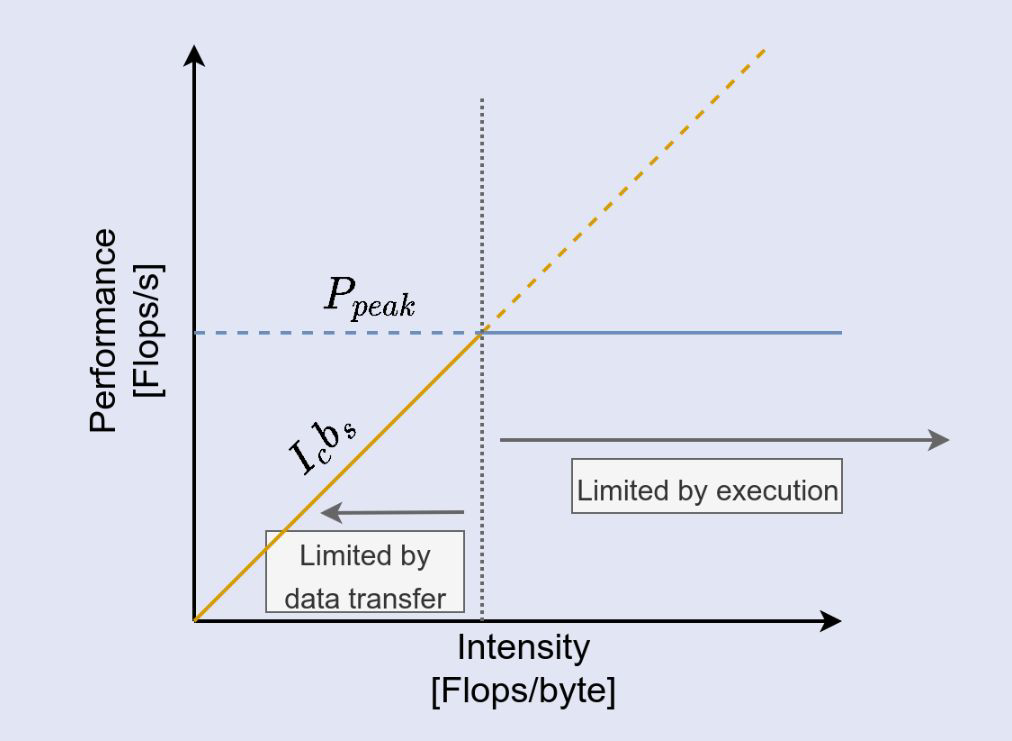
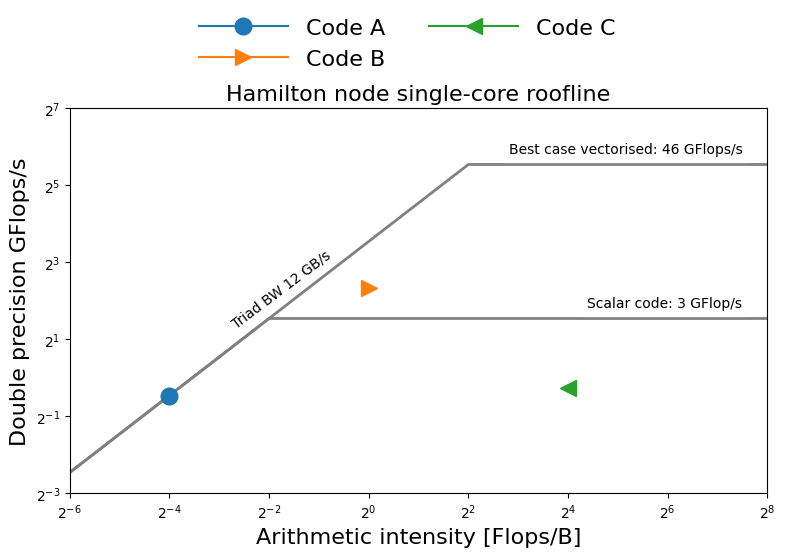
Roofline diagram

Applying roofline

Roofline characterises performance using three numbers:

• HW1. $P_{\text{peak}}$: peak floating point performance
• HW2. $b_s$: streaming memory bandwidth
• SW1. $I_c$: operational intensity of the code
• SW2. performance of the code

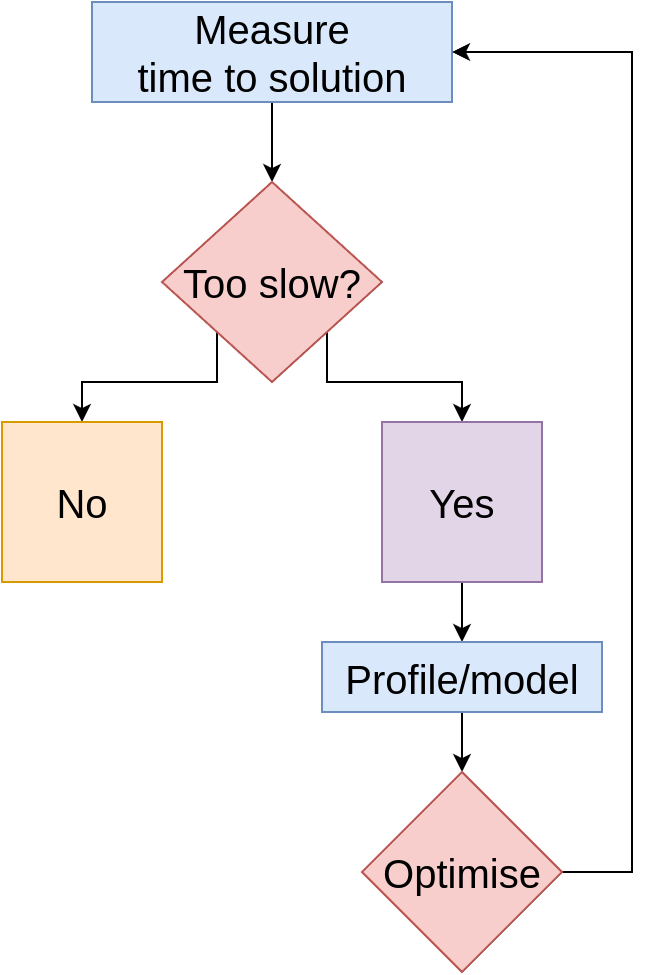
Process

1. Measure these numbers
2. Draw diagram
3. Use diagram to choose optimisations likely to pay off

Guide for optimisation choices

Determining the memory bandwidth

Data transfers are modeled with streaming memory bandwidth
Estimating streaming memory bandwidth (STB)

1. Computation
   • find out speed of memory $M_s$
   • find out number of memory channels $C$
   • STB in B/s is $C \times M_s \times 8$
     ⇒ speed of memory often unknown in practice
2. Measurement using STREAM
   • typical solution (see exercise 4)

Determining floating point throughput

Absolute peak can be estimated from

• specification sheet frequency
• knowledge of hardware architecture

AMD Zen 2 architecture (FPU)

• Floating point instructions execute on 4 ports
• Up to 4 “$\mu$ops” issued per cycle
• up to 2 floating point instructions per cycle
• MUL and FMA ($y ← a + b × c$) are issued on ports 0 and 1
• ADD are issued on ports 2 and 3
• DIV are only issued on port 3

Example

Assuming a maximum clock speed of 3.35GHz

Best case: For code with only double precision SIMD FMAs, peak throughput is

Only DIVs: Code only does double precision SIMD DIVs

Determining machine characteristics

• Sometimes multiple “roofs” for different instruction mixes
• Calculations are complicated by frequency scaling as well

More details

• https://wikichip.org for spec sheets
• https://uops.info for μops execution throughput
• Travis Down’s discussion on finding limiting factors in (simple) code

Computing operational intensity

Two options:

1. measurement using performance counters
2. pen-and-paper method
   • count floating point operations
   • count data accesses
   • use formula $I_C = \frac{M}{B} $ where
     • M is the number of Flops executed
     • B is the number of bytes moves

Assessing operational intensity

double *a, *b, *c, *d;
...;

for (int i = 0; i < N; i++) {
    for (int j = 0; j < M; j++) {
        a[j] = b[i]*c[i] + d[i]*a[j];
    }
}

Counting operations

• 3 double-precision Flops/iteration
• 3NM total double-precision Flops
• Notice we don’t care what operations these are

Counting data accesses

• Load counts as one access, write as two (one load, one store).
• 3 reads, 1 write per iteration.
• $8 × 3N + 8 × 2M$ total bytes.

A model of cache

Perfect cache

• Lower bound
• Data moved to cache once
• Counts unique memory accesses
• $8 \times 2M + 8 \times 3N$ total bytes

Pessimal cache

• Upper bound
• Each array access misses cache
• Counts total memory accesses

• $8 \times 2MN + 8 \times 3MN$ total bytes

• These bounds are typically not tight
• Better bounds normally require more work in the analysis
• Best employed in combination with measurement of operational intensity