PO Lecture 6 Cache blocking & tiling

PO Lecture 6 Cache blocking & tiling

Computing the matrix transpose

Given N-by-N matrices A and B, we can compute

$B_{ij} \leftarrow A_{ji}$

with

double *A, *B;
...
for (int i = 0; i < N; i++)
    for (int j = 0; j < N; j++)
        B[i*N + j] = A[j*N + i];

What is the performance of this code?

Matrix transpose: simple performance model

• N² stores
• N² loads
• no computation

What do you expect?

Load vs. Store

• Are loads and stores affected by cache locality in the same way?
  No
• For loads we mainly want to increase cache hits
• For stores, it is important due to cache coherence and depends on the writing policy
• It may be interesting to read more on non-temporal stores, e.g. here.

| Matrix size | bandwidth [GB/s] | | :———: | :————–: | | 128 × 128 | 22 | | 256 × 256 | 13 | | 512 × 512 | 13 | | 1024 × 1024 | 5 | | 2048 × 2048 | 1.6 | | 4096 × 4096 | 0.9 |

What went wrong?

for (int i = 0; i < N; i++)
    for (int j = 0; j < N; j++)
        B[i*N + j] = A[j*N + i];

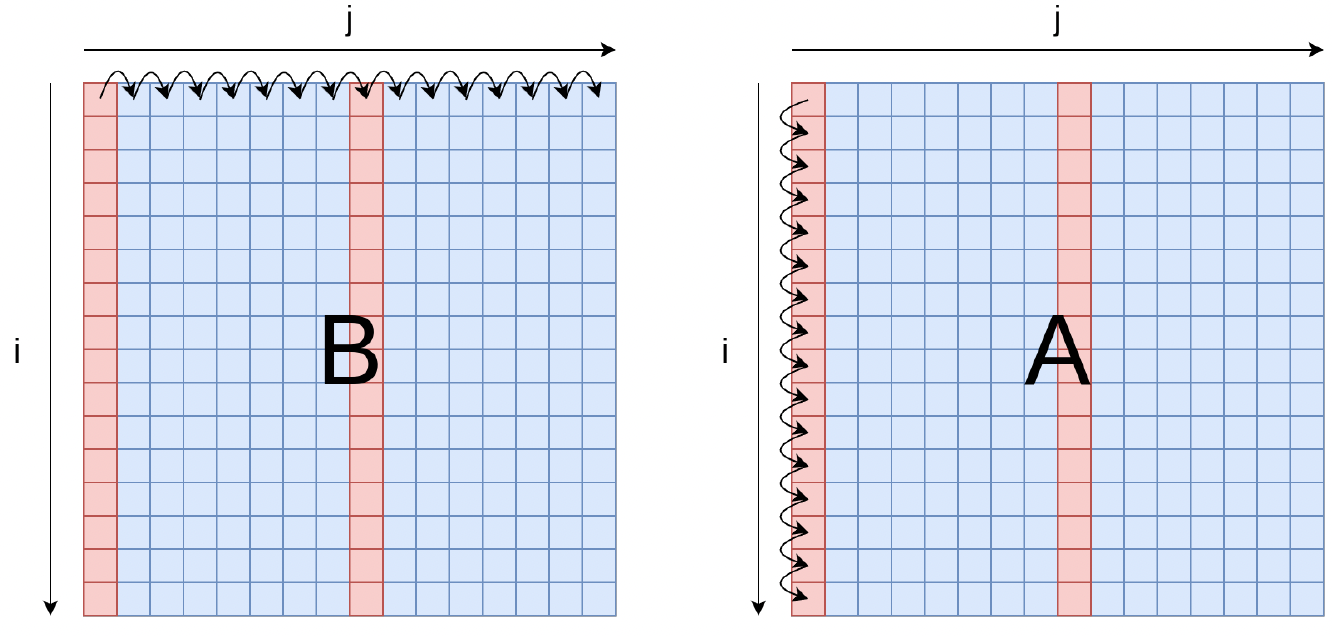
• Contiguous access to B, stride-N access to A
• If both matrices fit in cache, a reasonable model could be
  $T_{cache} = N^2(t_{read} + t_{write})$
• Reads of A load a full cache line, but use only 8 bytes:
  $T_{mem} = N^2(8t_{read} + t_{write})$

A picture

Cache locality

• Matrices are stored by rows
• Cache line size is L
• A has strided access
• We need LN/8 cache to get reuse
• We can reorder the iterations to preserve spatial locality

Idea

• Break loop iteration space into blocks
  1. strip mining
  2. loop reordering

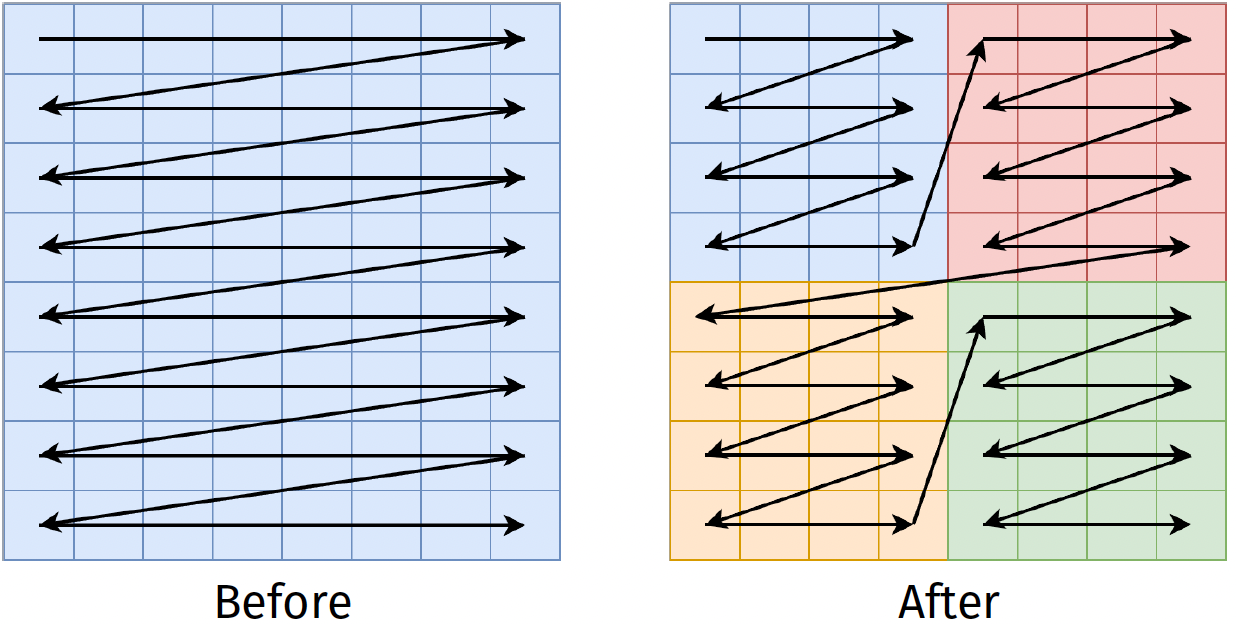
Strip mining

Before

• actually faster

for ( int i = 0; i < N; i++ )
    A[i] = f(i);

After

for ( int ii = 0; ii < N; ii += stride)
    for ( int i = ii; i < min(N, ii + stride); i++)
        A[i] = f(i);

Mostly useful for nested loops

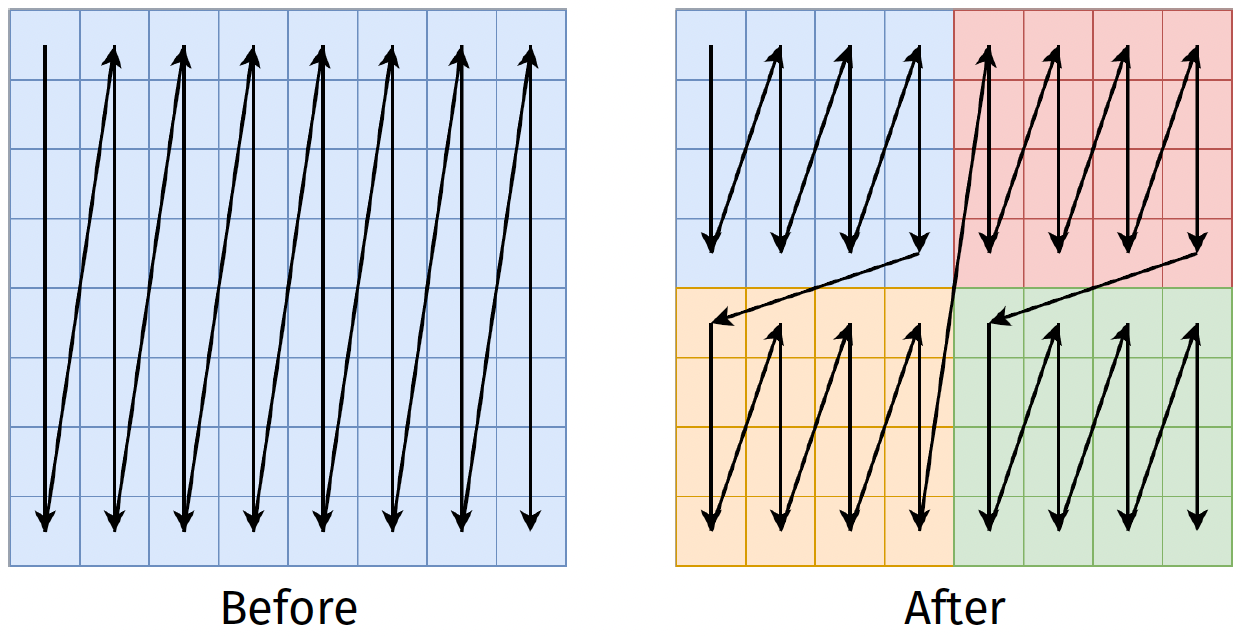
Strip mining nested loops

Before

for (int i = 0; i < N; i++)
    for (int j = 0; j < N; j++)
        B[i*N + j] = A[j*N + i];

After

for (int ii = 0; ii < N; ii += stridei)
    for (int i = ii; i < min(N, ii+stridei); i++)
        for (int jj = 0; jj < N; jj += stridej)
            for (int j = jj; j < min(N, jj+stridej); j++)
                B[i*N + j] = A[j*N + i];

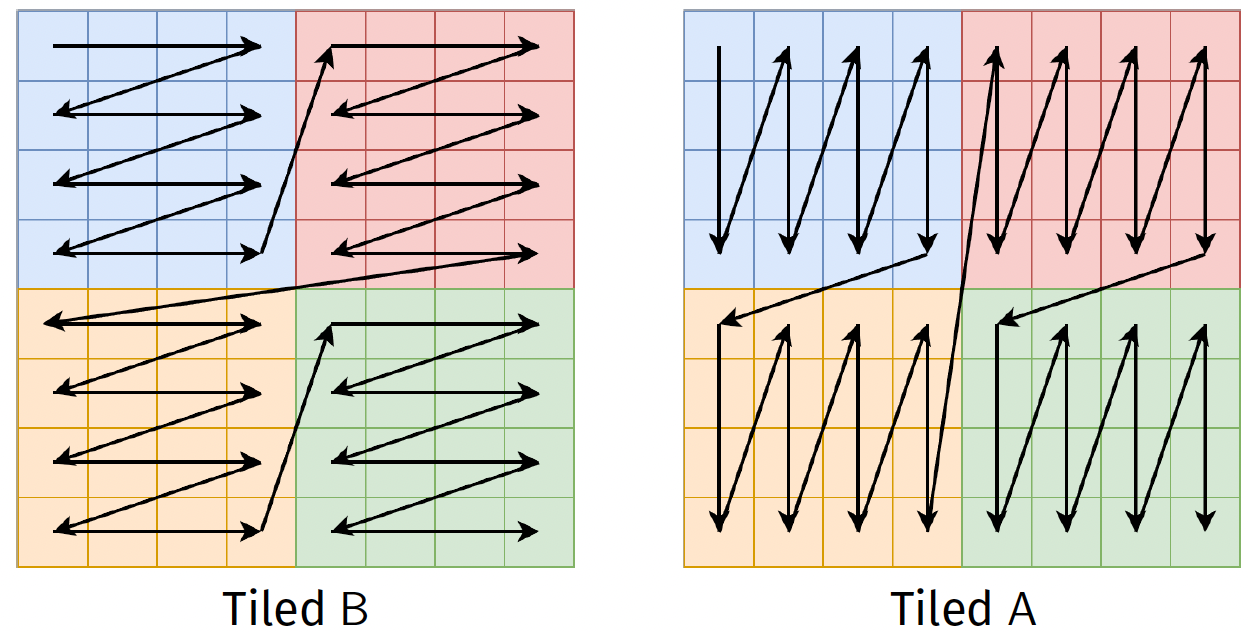
Reordering loops

After permuting i and jj loops

for (int ii = 0; ii < N; ii += stridei)
    for (int jj = 0; jj < N; jj += stridej)
        for (int i = ii; i < min(N, ii+stridei); i++)
            for (int j = jj; j < min(N, jj+stridej); j++)
                b[i*N + j] = a[j*N + i];

• Two free parameters stridei and stridej
• Need to choose according cache hierarchy
• Ideally block for L1, L2, L3
• The extra logic adds some overhead

Iteration over B

Iteration over A

Comparison

Exercise 7: Tiled matrix transpose

1. Split into small groups
2. Download the two versions of the code
3. Measure bandwidth as matrix size changes
4. Try different tile sizes
5. Ask questions!