PO Lecture 2 Memory Hierarchy

作业回顾

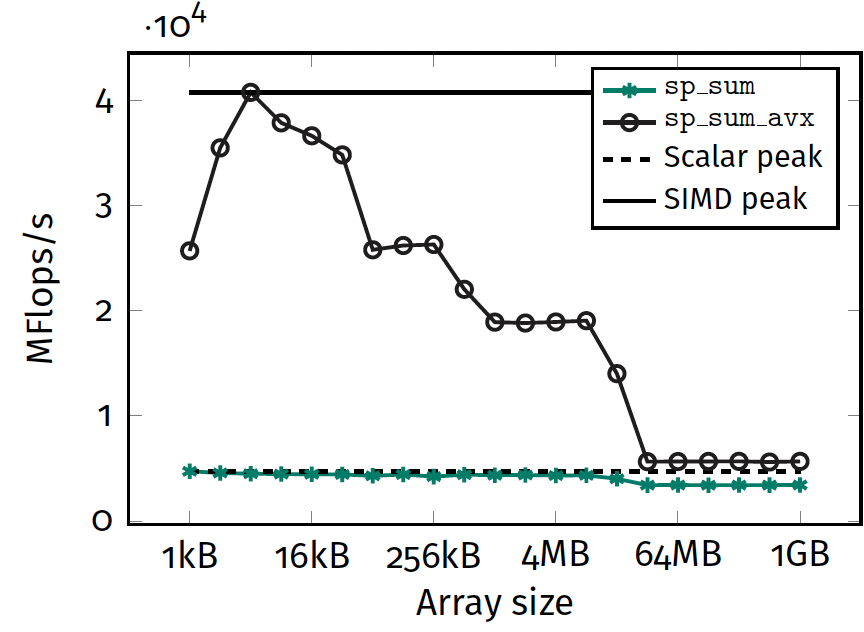
Sum reduction benchmark (Exercise 1)

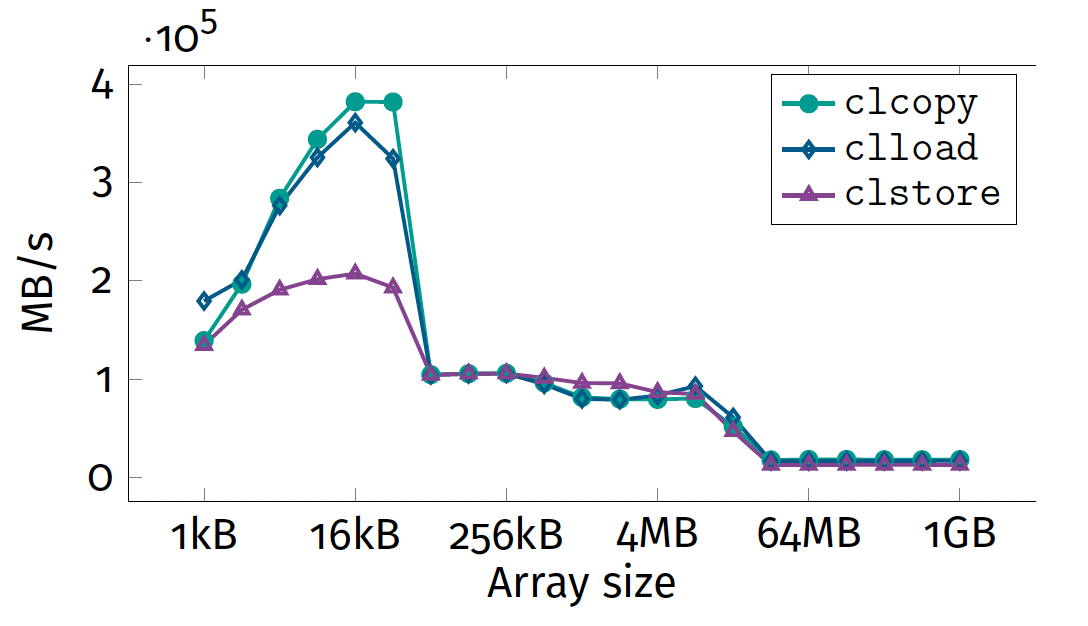
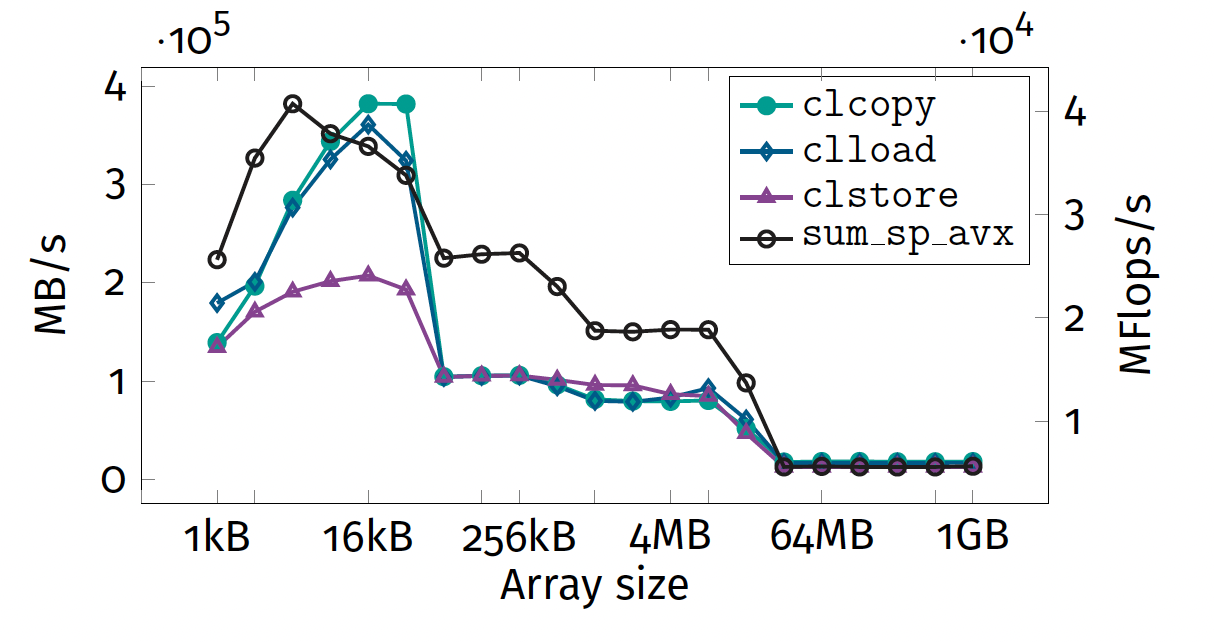
• SIMD: 4 plateaus
• scalar: 3 plateaus

Performance peak

Variability This is due to CPU Boosting.

Question SIMD code does not achieve theoretical peak for all sizes. Why?

Hardware bottlenecks

• Cannot be instruction throughput.
• Memory bandwidth decreases with vector siz

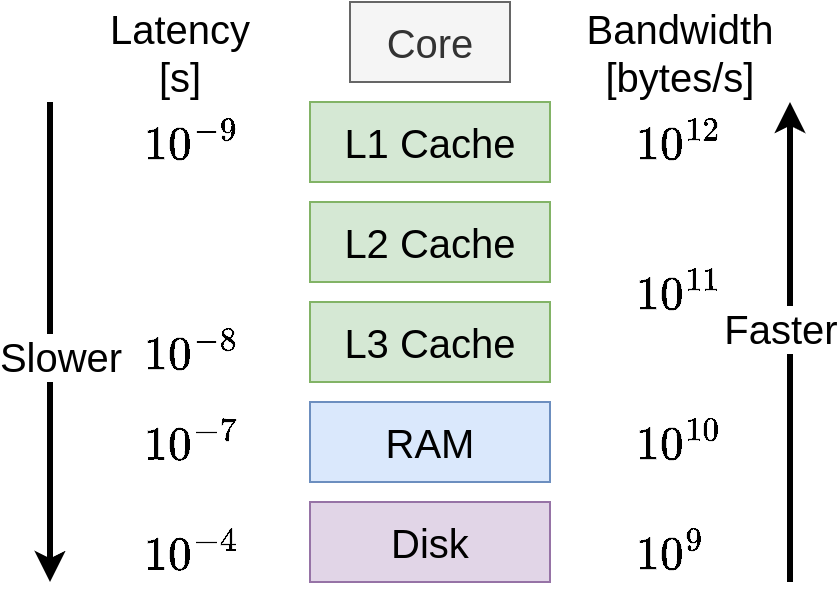
Memory Hierarchy

Two types of memory:
▶ small and fast
▶ large and slow

Large and fast is impossible:
⇒ physics gets in the way.

Optimisation: refactor algorithms to keep data in fast memory.
Check Colin Scott’s page for more detail on latencies.

Cache memory: overview

Features

• Hierarchy of small, fast memory.
• Keep a copy of frequently used data for faster access.

Issues

• Frequently accessed data not known a priori.
• Only heuristics are possible → principle of locality.

Principle of locality

• Frequently accessed data often unknown before execution
• In practice, most programs exhibit locality of data access.
• Optimised algorithms attempt to exploit this locality.

Temporal locality If I access data at some memory address, it is likely that I will do so again “soon”.

Spatial locality If I access data at some memory address, it is likely that I will access neighbouring addresses.

Temporal locality

On first access to a new address, the data is:

• loaded from main memory to registers
• stored in cache

Temporal locality

On first access to a new address, the data is:

• loaded from main memory to registers
• stored in cache

Trade-off solution:

• Small performance penalty for first access (storing is not free)
• Subsequent accesses use cached copy and are much faster.

Spatial locality

On first access to a new address, the data is:

• loaded from main memory to registers
• stored in cache
• neighbouring addressed are also stored in cache

Trade-off solution:

• Large performance penalty for first access
• Subsequent accesses to neighbouring data will be fast

Example: sum reduction

float s[16] = 0;
for (i = 0; i < N; i++)
    s[i%16] += a[i];

• Temporal locality
  • 16 entries of s are accessed repeatedly
  • Makes sense to keep all of s in cache
• Spatial locality
  • Contiguous entries of a are accessed
  • When loading a[i] it makes sense to load a[i+1] too.

Designing a cache

Important questions

1. When we load data into the cache, where do we put it?
2. If we have an address, how do determine if it is in the cache?
3. What do we do when the cache becomes full?

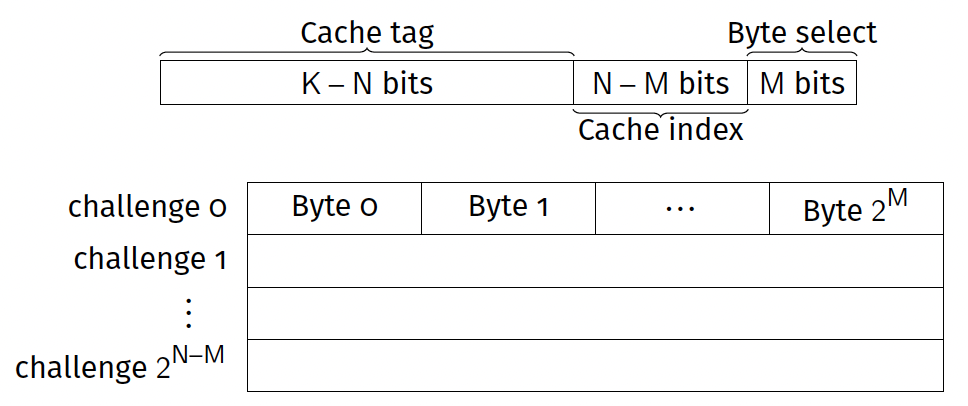
• Each datum uniquely referenced by its K-bit address
• Need to turn this large memory address into a cache location
• K is typically large ($2^{32} / 2^{64}$ addresses)

Direct mapped cache

• Cache can store $2^N$ bytes
• Divided into challenges (or cache lines) each of $2^M$ bytes
• Each address references one byte
• Use N bits of address to select which slot in the cache to use

Simplest solution: injection from RAM to cache

Direct mapped caches: indexing

• Byte select: Use lowest M bits to select correct byte in challenge.
• Cache index: Use next N – M bits to select correct challenge.
• Cache tag: Use remaining K – N bits as a key.

Choice of cache line size

• Data is loaded one cache line at a time
• Immediately exploits spatial locality
• Larger cache lines are not always better
• Almost all modern CPUs use 64-byte size

Rule of thumb Cache-friendly algorithms work on cache line-sized chunks of data.

Direct mapped caches: eviction

• Conflict: two addresses have the same low bit pattern
• Resolution: newest loaded address wins.
• This is a least recently used (LRU) eviction policy.

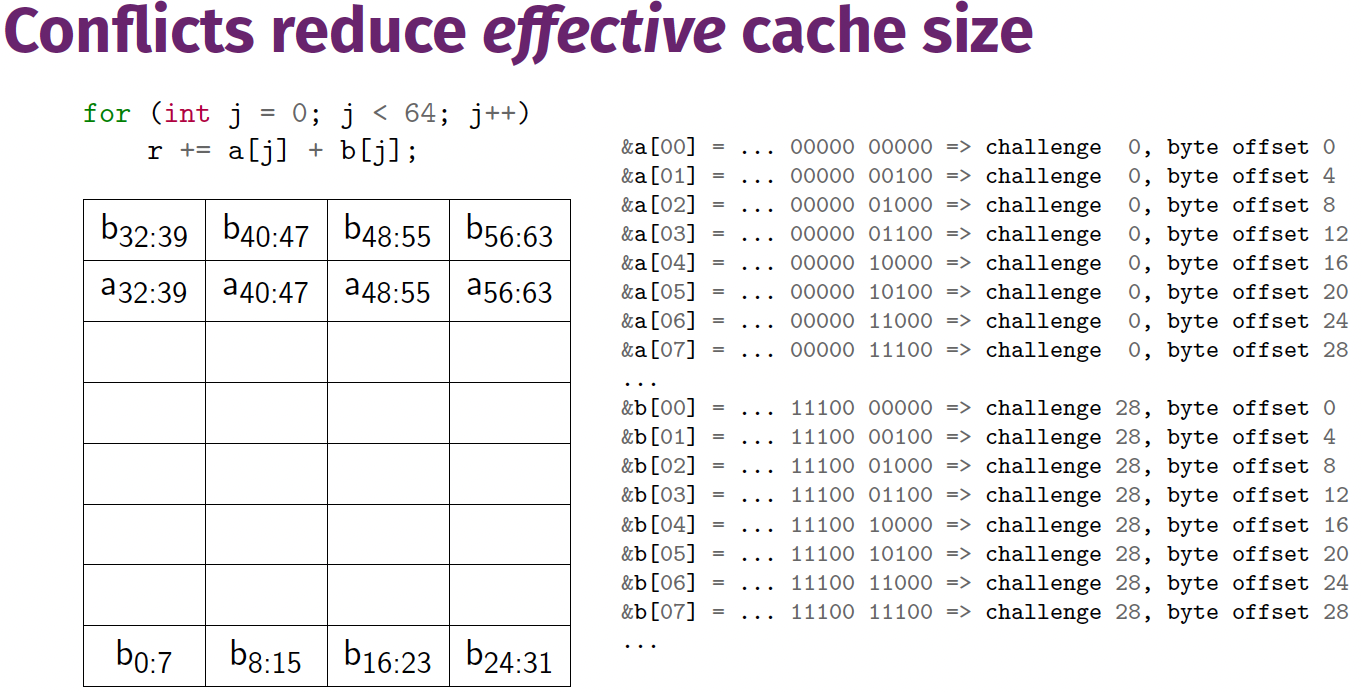
What can go wrong?

int a[64], b[64], r = 0;
for (int i = 0; i < 100; i++)
    for (int j = 0; j < 64; j++)
        r += a[j] + b[j];

• 1KB cache
• 32-byte challenge size
• So N = 10, M = 5
• 32 challenges in the cache

Conflicts reduce effective cache size

Cache thrashing

What can go wrong?

int A[64], B[64], r = 0;
for (int i = 0; i < 100; i++)
    for (int j = 0; j < 64; j++)
        r += A[j] + B[j];

• 1KB cache
• 32 byte challenge size

• So N = 10, M = 5. 32 challenges in the cache.

• We need $2 \cdot 64 \cdot 4 = 512$ bytes to store A and B in cache.
• This only requires 16 challenges, so our cache is large enough.
• If low bits of addresses match, same cache lines are mapped.
• In the worst case, every load of $B[j]$ evicts $A[j]$, and vice versa.

Cache associativity

• Direct mapped
  • Each RAM challenge maps to exactly one cache line.
  • LRU eviction policy (new data overwrite old)
• Fully associative
  • Each RAM byte can map to any cache line
  • Data is stored in first unused cache line
  • If all lines are used, overall LRU one is replaced
  • Most flexible, but also most expensive

k-way set associative cache

• k “copies” of a direct mapped cache.
• Each challenge from main memory maps to k cache lines, called sets.
• Typically use LRU eviction.
• Usual choice: N ∈ {2, 4, 8, 16}.
• Skylake has N = 8 for L1, N = 16 for L2, N = 11 for L3.

Exercises 2/3: memory bandwidth/saturation

1. Split into small groups

2. Make sure one person per group has access to Hamilton

3. Benchmark memory bandwidth as a function of vector size

4. You can use the bash script from last week.

5. Ask questions!

Exercise 2: results

[[2025-01-20-PO-3]]