Post

Robotics 4 - Kinematics

Posted Updated
By
7 min read
Robotics 4 - Kinematics

From @VergilOP

Lecture 4 - Kinematics

Learning Objectives

Objectives:

  1. Spatial Description
  2. Transformation
  • Rotation
  • Translation

Spatial Description 空间描述

  • Position of a Point 点的位置
    • With respect to a fixed origin O, the position of a point P is described by the vector OP(p)
      相对于固定原点 O，点 P 的位置由向量 OP(p) 描述
  • Coordinate Frames:
    • Rotation
    • Translation
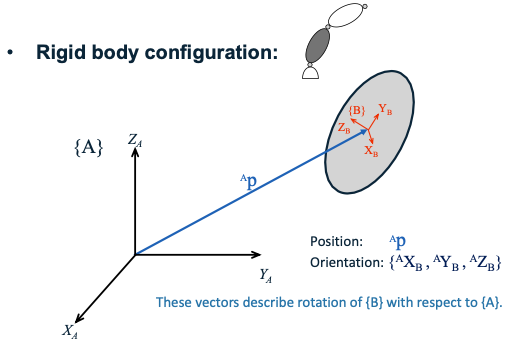
  • Rigid body configuration:
    • Position: $^AP$
    • Orientation: ${^AX_B, ^AY_B, ^AZ_B}$

These vectors describe rotation of {B} with respect to {A}

image-20241128181058807

Transformation

Rotation

image-20241128181850706

  • Rotation Matrix:

    旋转矩阵（Rotation Matrix）用于描述坐标系之间的旋转关系。假设有两个坐标系${A}$和${B}$，旋转矩阵$^A_BR$表示从坐标系${B}$到坐标系${A}$的旋转。 \(^A_BR = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} = \begin{bmatrix} ^A \hat{X}_B & ^A \hat{Y}_B & ^A \hat{Z}_B \end{bmatrix} = \begin{bmatrix} {^B \hat{X}_A}^T \\ {^B \hat{Y}_A}^T \\ {^B \hat{Z}_A}^T \end{bmatrix} = {^B_A R}^T = \begin{bmatrix} \hat{X}_B \cdot \hat{X}_A & \hat{Y}_B \cdot \hat{X}_A & \hat{Z}_B \cdot \hat{X}_A\\ \hat{X}_B \cdot \hat{Y}_A & \hat{Y}_B \cdot \hat{Y}_A & \hat{Z}_B \cdot \hat{Y}_A\\ \hat{X}_B \cdot \hat{Z}_A & \hat{Y}_B \cdot \hat{Z}_A & \hat{Z}_B \cdot \hat{Z}_A \end{bmatrix}\)

    表达式 基向量组合形式 转置形式 点积形式

    $^B \hat{X}_A$表示在坐标系${B}$中，坐标系${A}$的X轴单位向量。同理，其他项以此类推。

    $\hat{X}_B$、$\hat{Y}_B$、$\hat{Z}_B$是坐标系${B}$的单位基向量，$\hat{X}_A$、$\hat{Y}_A$、$\hat{Z}_A$是坐标系${A}$的单位基向量。

    旋转矩阵是一个正交矩阵（Orthogonal Matrix），其转置等于其逆矩阵。

    • Inverse of Rotation Matrix(Orthonormal Matrix) \(^A_BR^{-1} =\ ^B_AR =\ ^A_BR^T\)

  • State description: $^A\hat{X}_B = ^A_BR\ \ ^B\hat{X}_B$

\[^A \hat{X}_B = {^A_B R} \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}\\ ^A \hat{Y}_B = {^A_B R} \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}\\ ^A \hat{Z}_B = {^A_B R} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\]

  • Dot product: 通过点积，可以计算基向量在不同坐标系中的投影关系。 \(^A \hat{X}_B = \begin{bmatrix} \hat{X}_B \cdot \hat{X}_A \\ \hat{X}_B \cdot \hat{Y}_A \\ \hat{X}_B \cdot \hat{Z}_A \end{bmatrix}\\ ^A \hat{Y}_B = \begin{bmatrix} \hat{Y}_B \cdot \hat{X}_A \\ \hat{Y}_B \cdot \hat{Y}_A \\ \hat{Y}_B \cdot \hat{Z}_A \end{bmatrix}\\ ^A \hat{Z}_B = \begin{bmatrix} \hat{Z}_B \cdot \hat{X}_A \\ \hat{Z}_B \cdot \hat{Y}_A \\ \hat{Z}_B \cdot \hat{Z}_A \end{bmatrix}\) 其中，每个元素表示${B}$的基向量在${A}$的基向量方向上的投影。例如，$\hat{X}_B \cdot \hat{X}_A$表示${B}$的X轴在${A}$的X轴方向上的投影。

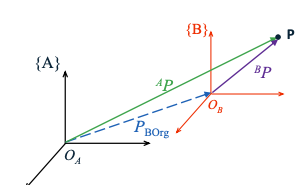
  • Description of a Frame:

    • 描述一个坐标系需要知道其基向量和原点位置：
      • 坐标系${B}$在${A}$中的表示包括：
        • 基向量：$^A \hat{X}_B$、$^A \hat{Y}_B$、$^A \hat{Z}_B$
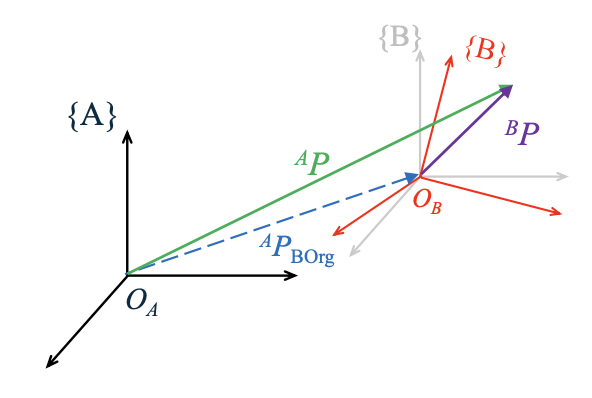
        • 原点位置：$^A P_{B_{\text{org}}}$
    • Frame{B}: $^A \hat{X}B$, $^A \hat{Y}_B, ^A \hat{Z}_B$, $^AP{Borg}$
      • 这里，$^A_BR$是从${B}$到${A}$的旋转矩阵，$^A P_{B_{\text{org}}}$是${B}$的原点在${A}$坐标系中的位置向量。
\[\{B\} = \{^A_BR\space\space^AP_{Borg}\}\]

  • Mapping:

    • Changing descriptions from frame to frame
    • 映射是指将一个向量从一个坐标系转换到另一个坐标系。
    • 旋转变换：
      • 当我们知道向量在${B}$坐标系中的表示$^B P$，想要得到它在${A}$坐标系中的表示$^A P$，可以使用旋转矩阵进行变换。

  • Rotations
    image-20241128182650612

    • 假设有一个向量$P$，它在坐标系${B}$中的表示为$^B P$。我们想要计算它在坐标系${A}$中的表示$^A P$。
      • 首先，利用${B}$和${A}$的基向量之间的关系：
    • If $P$ is in ${B}$: $^BP$
    \[^AP = \begin{bmatrix} ^B \hat{X}_A. ^BP \\ ^B \hat{Y}_A. ^BP \\ ^B \hat{Z}_A. ^BP \end{bmatrix} = \begin{bmatrix} ^B \hat{X}_A^T \\ ^B \hat{Y}_A^T \\ ^B \hat{Z}_A^T \end{bmatrix} \cdot\ ^BP\]

    \(^AP =\ ^A_BR\ ^BP\)

    • 这意味着，可以直接使用旋转矩阵$^A_BR$将向量从${B}$坐标系转换到${A}$坐标系。

Translation 平移

image-20241128182749914

\[^AP_{OA} = ^AP_{OB} + ^AP_{BOrg}\]

General Transformation

image-20241129103914524

\[^AP =\ ^A_BR\ ^BP +\ ^AP_{Borg} \\\] \[\begin{bmatrix} ^AP \\ 1 \end{bmatrix} = \begin{bmatrix} ^A_BR &\ ^AP_{Borg} \\ 0\ 0\ 0 & 1 \end{bmatrix} = \begin{bmatrix} ^BP\\ 1 \end{bmatrix}\]

$^A P$：点$P$在坐标系${A}$中的表示。

$^B P$：点$P$在坐标系${B}$中的表示。

$^A_B R$：从${B}$到${A}$的旋转矩阵。

$^A P_{B_{\text{org}}}$：坐标系${B}$的原点在${A}$中的位置。

  • Homogeneous Transformation: 齐次变换矩阵

    统一旋转和平移 \(^AP_{(4\times1)} =\ ^A_BT_{(4\times4)}\ ^BP_{(4\times1)}\)

$^A_B T$是齐次变换矩阵，包括旋转和平移。

  • General Operators: \(P_2 = \begin{bmatrix} R_k(\theta) & Q \\ 0\ 0\ 0 & 1 \end{bmatrix}P_1\)

    \[P_2 = T\ P_1\]

$P_1$：初始点的齐次坐标表示。

$P_2$：变换后的点的齐次坐标表示。

$R_k(\theta)$：绕轴$k$旋转$\theta$角度的旋转矩阵。

$Q$：平移向量。

  • Inverse Transform 逆变换 \(^A_B T = \begin{bmatrix} ^A_B R & ^A P_{Borg} \\ 0\ 0\ 0 & 1 \end{bmatrix}\)

    \[^A_B T^{-1} = ^B_A T = \begin{bmatrix} ^A_B R^T & -^A_B R^T \cdot\ ^AP_{Borg} \\ 0\ 0\ 0 & 1 \end{bmatrix}\]

  • Homogeneous Transform Interpretations:

  • Description of a frame 坐标系的描述 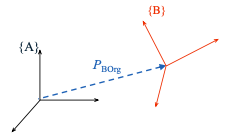image-20241128184251000 \(^A_BT:\{B\} = \{^A_BR\ \ ^AP_{Borg}\}\)

  • Transform mapping 坐标的映射 image-20241128184321955 \(^A_BT:\ ^BP \rightarrow\ ^AP\)

  • Transform operator 变换算子 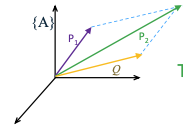image-20241128184351713 \(T: P_1 \rightarrow P_2\) $P_1$：初始点。

    $P_2$：经过变换后的点。

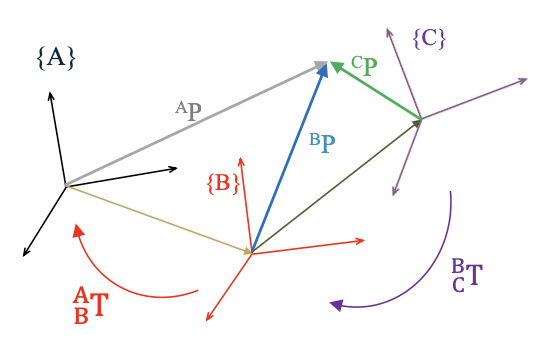
  • Compound Transformation:复合变换

    image-20241129105316388

    \[^BP = ^B_C T \ C_P\] \[^AP = ^A_B T \ B_P\] \[^AP = ^A_B T \ ^B_C T \ C_P\] \[^A_C T = ^A_B T \ ^B_C T\] \[^A_C T = \begin{bmatrix} ^A_B R \ ^B_C R & ^A_B R \ ^B P_{Corg} + ^A P_{Borg} \\ 0\ 0\ 0 & 1 \end{bmatrix}\]

  • Transform Equation

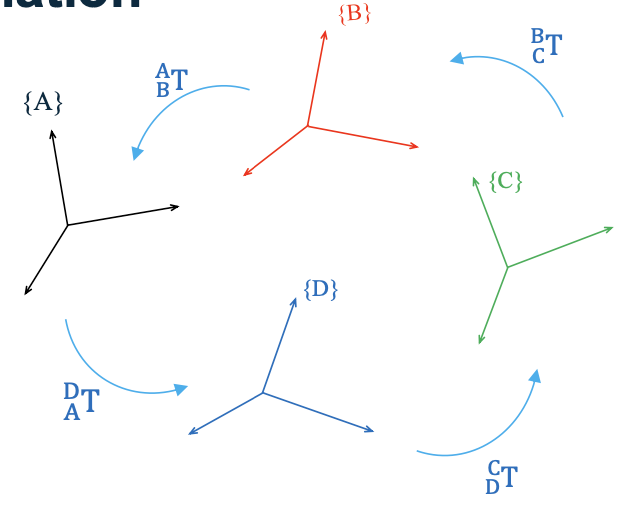
    image-20241129105332226

    • 在多个坐标系之间的循环变换中，变换矩阵的乘积应等于单位矩阵：
    \[^A_B T \ ^B_C T \ ^C_D T \ ^D_A T = I\]

Representations

  • End-effector Configuration 末端执行器的齐次变换矩阵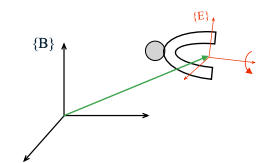： image-20241128184422332 \(^B_ET: Position + Orientation\) $^B_E T$表示末端执行器相对于基座坐标系${B}$的齐次变换矩阵，包含了位置和姿态的信息

  • End-effector configuration parameters: \(X = \begin{bmatrix} X_P \\ X_R \end{bmatrix}\) $X_P$：位置参数，表示末端执行器在空间中的位置。

    $X_R$：姿态参数，表示末端执行器在空间中的方向或旋转。

  • Position representation:
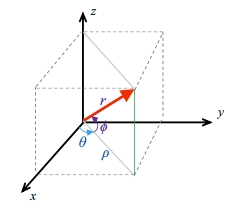
    image-20241128184447886

    • Cartesian: (x, y, z) 笛卡尔坐标系
    • Cylindrical: $(\rho, \theta, z)$ 圆柱坐标系
    • Spherical: $(r, \theta, \phi)$ 球坐标系
Study, Master
DU Robotics
This post is licensed under CC BY 4.0 by the author.

Trending Tags

DU AI ML CV Robotics GPU HPC ASML PO UL