Robotics 5 - Manipulator Kinematics

From @VergilOP

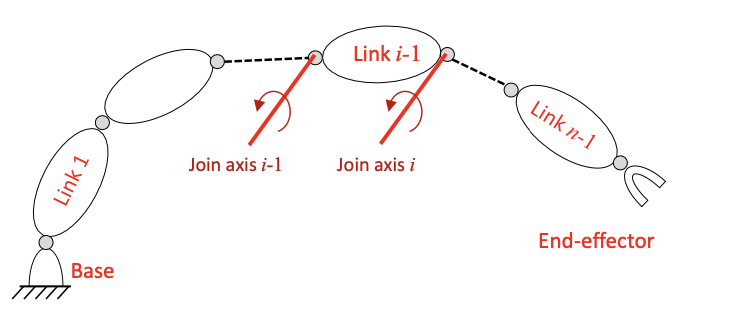
Lecture 5 - Manipulator Kinematics

Learning Objectives

• Objectives
  • Link Description
  • Denavit-Hartenberg(D-H parameters)
  • Manipulator Kinematics

Link Description

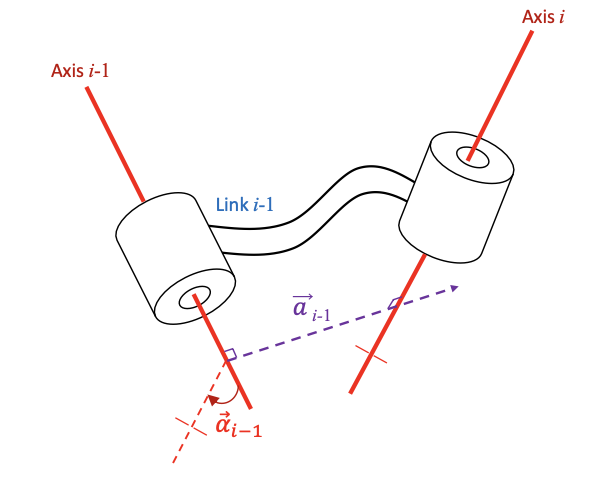
• $\vec{a}_{i-1}$: Link Length - mutual perpendicular 连杆长度
• $\vec{\alpha}_{i-1}$: Link Twist - angle between axes轴 $i$ and $i-1$ 连杆扭角

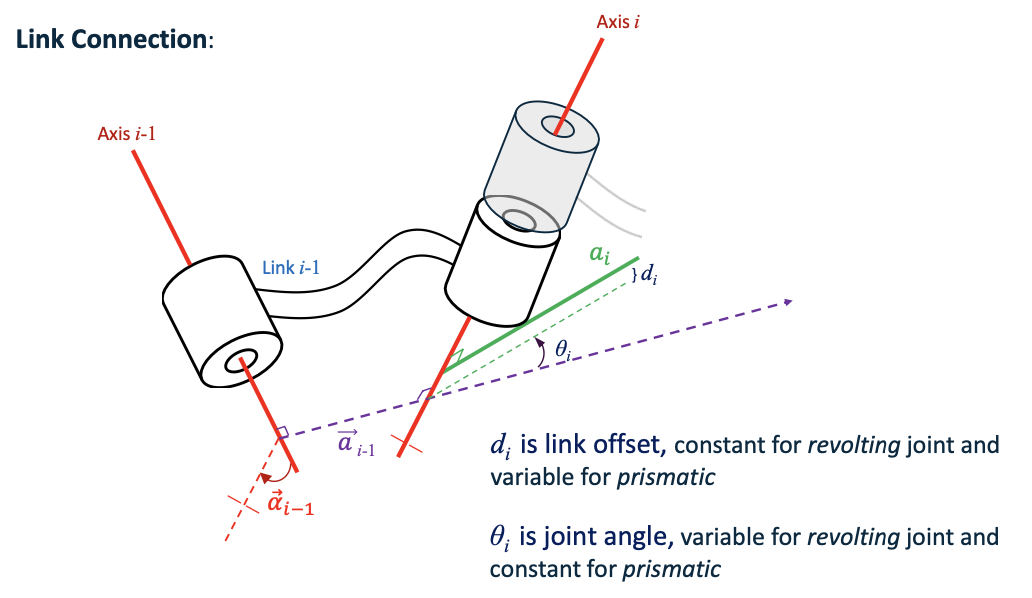
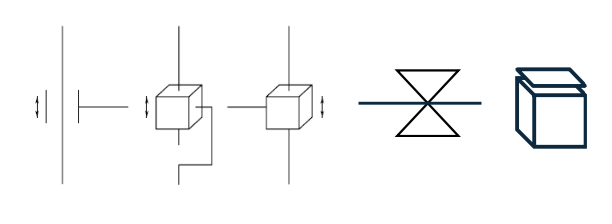
Link Connection:

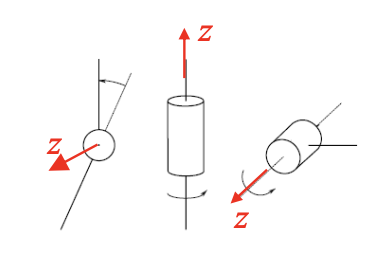
• $d_i$ is link offset, constant for revolting joint and variable for prismatic 关节偏距

  • 定义：$d_i$是沿着$Z_i$轴，从$X_{i-1}$轴移动到$X_i$轴所需的距离。

    特性：

    • 对于旋转关节：$d_i$是一个常数，因为旋转关节的运动不影响沿$Z_i$轴的距离。
    • 对于移动关节：$d_i$是一个变量，因为移动关节的运动就是沿$Z_i$轴的线性移动。

• $\theta_i$ is joint angle, variable for revolting joint and constant for prismatic 关节角度

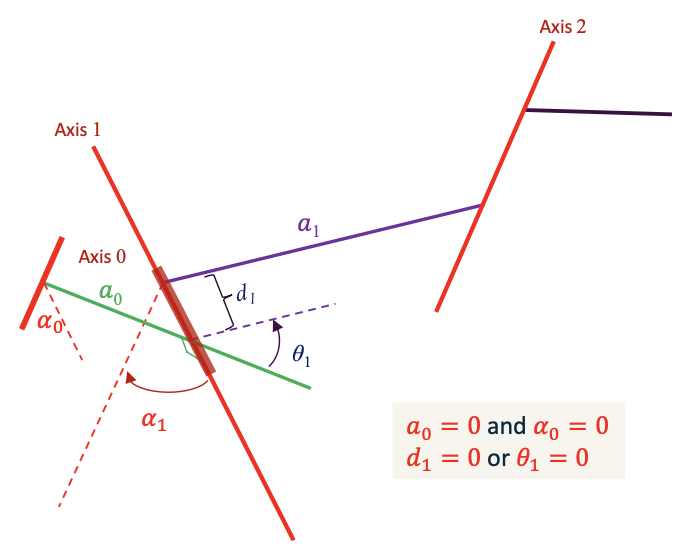
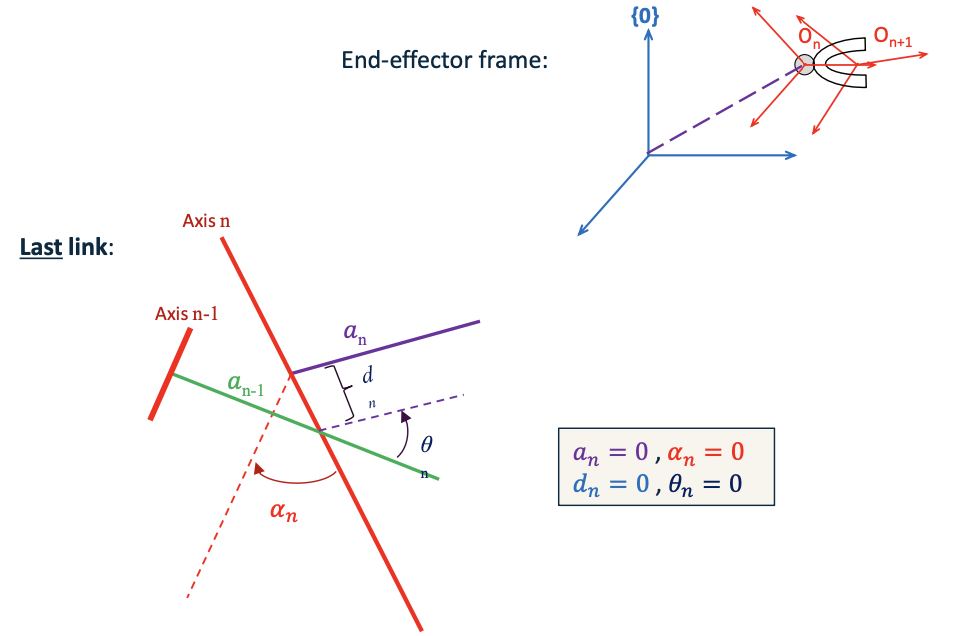
First and last links:

$a_i$ and $\alpha_i$ depend on joint axes $i$ and $i + 1$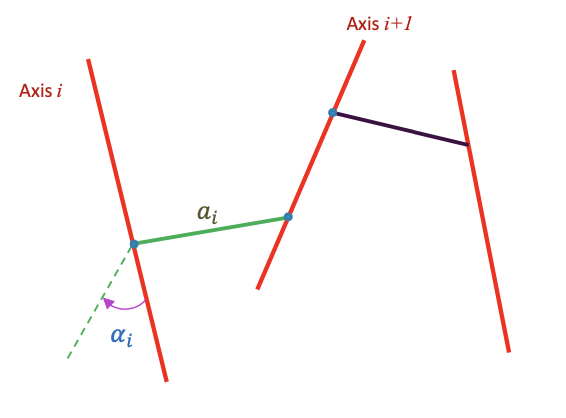

Convention: \(a_0 = a_n = 0 \text{ and } \alpha_0 = \alpha_n = 0\)

• First link:
  

• Last link:
  

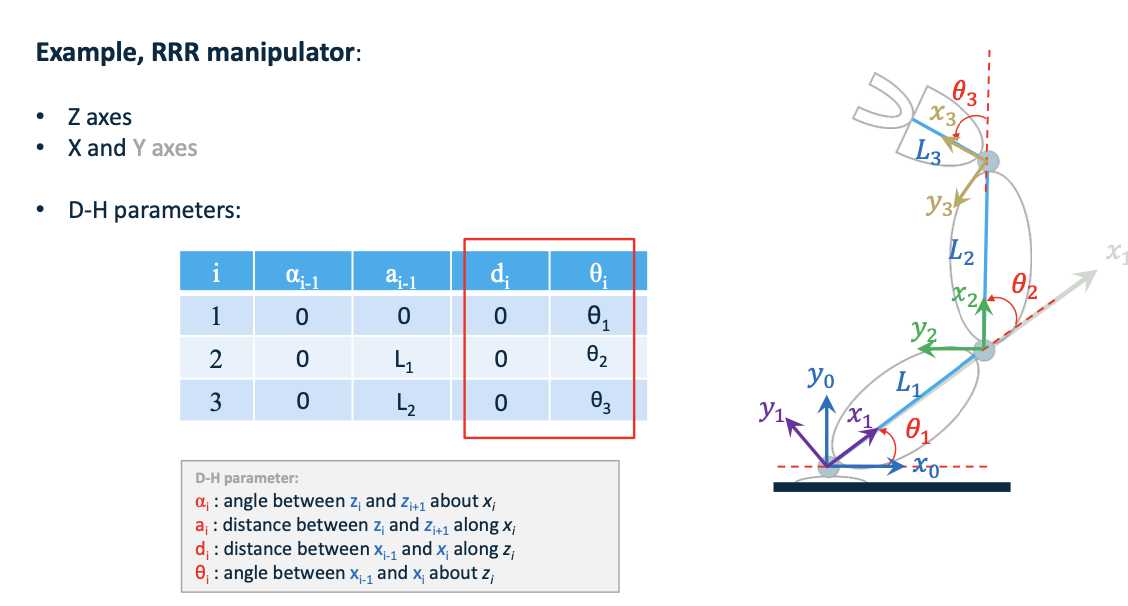
• Denavit-Hartenberg(D-H) Parameters:
  • Four D-H parameters are $(\alpha_i, a_i, d_i, \theta_i)$
• Three fixed link parameters and
• One joint variable:
• \[\left\{\begin{array}{ll}\theta_i & \text{Revolute joint} \\ Sd_i & \text{Prismatic joint}\end{array}\right.\]

• $\alpha_i$ and $a_i$ describe the link $i$
• $d_i$ and $\theta_i$ connection between the links

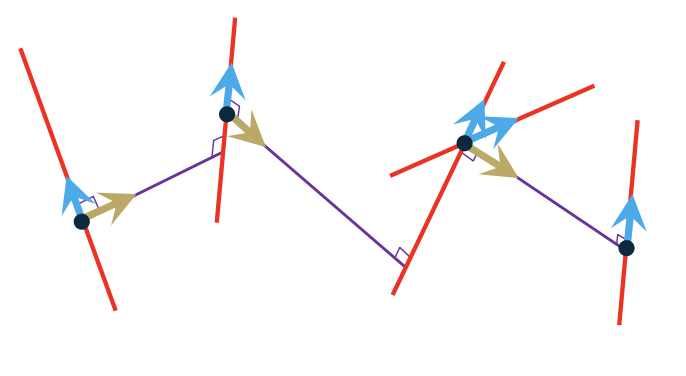
Frame attachment

1. Common Normals
2. Origins
3. Z-axis
4. X-axis

Summary

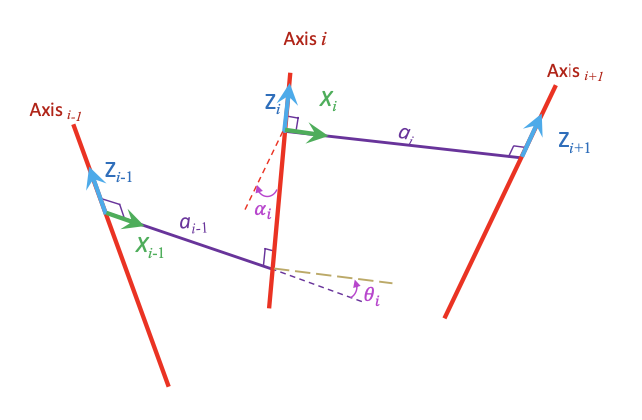
$\alpha_i$: angle between $z_i$ and $z_{i+1}$ about $x_i$

$a_i$: distance between $z_i$ and $z_{i+1}$ along $x_i$

$d_i$: distance between $x_{i-1}$ and $x_i$ along $z_i$

$\theta_i$: angle between $x_{i-1}$ and $x_i$ about $z_i$

• Forward Kinematics:
  \(^{i-1}_iT = ^{i-1}_RT\ ^R_QT\ ^Q_PT\ ^P_iT\)

  \[{}^{i-1}_i T(\alpha_{i-1}, a_{i-1}, \theta_i, d_i) = R_x(\alpha_{i-1}) D_x(a_{i-1}) R_z(\theta_i) D_z(d_i)\] \[{}^{i-1}_i T = \begin{bmatrix} c\theta_i & -s\theta_i c\alpha_{i-1} & s\theta_i s\alpha_{i-1} & a_{i-1} c\theta_i \\ s\theta_i & c\theta_i c\alpha_{i-1} & -c\theta_i s\alpha_{i-1} & a_{i-1} s\theta_i \\ 0 & s\alpha_{i-1} & c\alpha_{i-1} & d_i \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

• Symbols:

  • Revolute Joints:
    
  • Prismatic joints: