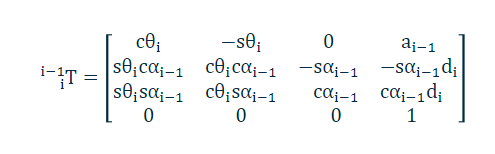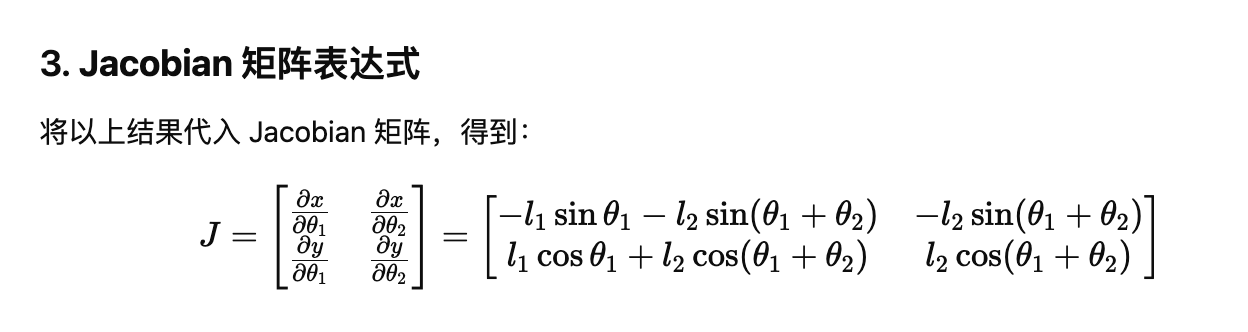Robotics Review

Posted Dec 2, 2024 Updated Dec 11, 2024

4 min read

10倒计算题

L2 气缸压力
机械臂关节自由度冗余度
坐标系变换 transformation 旋转矩阵
alpha a d theta Manipulator Kinematics
车 omega 差速
高斯误差 s x t theta
hk sk qk
雅可比矩阵 (带入?)
? Localisation
？？控制 PID
A* 路径规划
Probabilistic Mapping 算概率

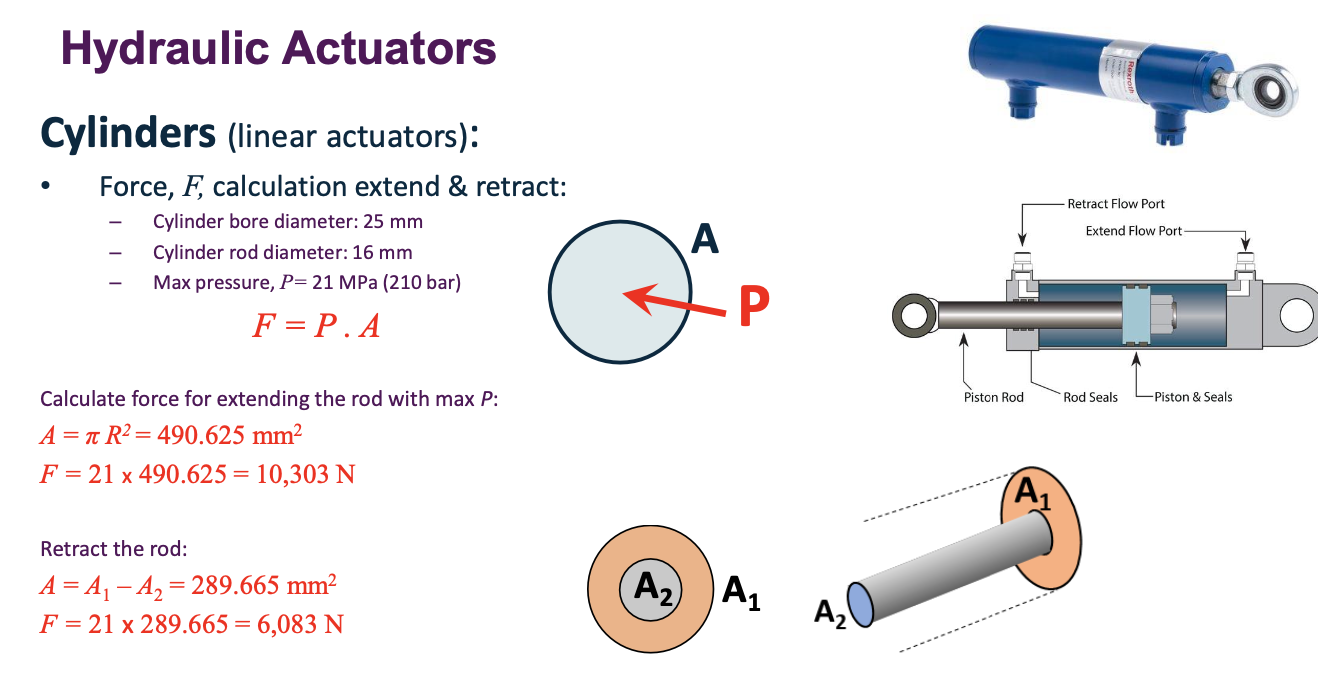
1 Cylinders

2

每个刚体需要 6 个参数来描述 – 3 个位置 – 3 个方向

n 个移动连杆 → 6n 个参数 n 个关节 → 5n 个约束有多少个自由度？ 6n – 5n = n 个自由度

$m_0$是末端执行器的自由度

max -> 6

冗余度 (n > m) n - m

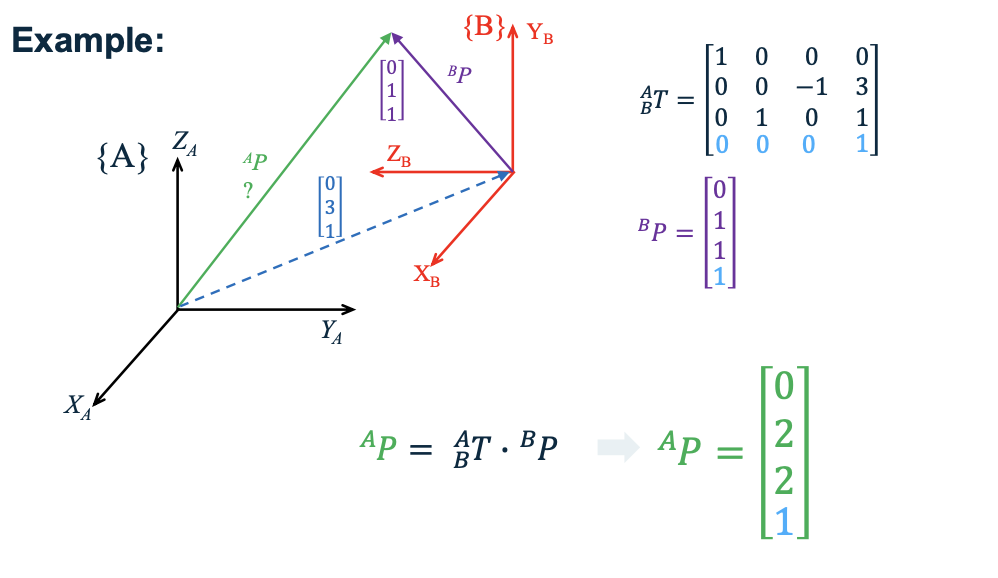
3 坐标系变换旋转矩阵

$^B_AR$ 坐标系A到坐标系B的旋转矩阵

\[^AP =\ ^A_BR\ ^BP +\ ^AP_{Borg} \\\] \[\begin{bmatrix} ^AP \\ 1 \end{bmatrix} = \begin{bmatrix} ^A_BR &\ ^AP_{Borg} \\ 0\ 0\ 0 & 1 \end{bmatrix} = \begin{bmatrix} ^BP\\ 1 \end{bmatrix}\]

eg.

Inverse Transform 逆变换 $^A_B T = \begin{bmatrix} ^A_B R & ^A P_{Borg} \\ 0\ 0\ 0 & 1 \end{bmatrix}$
\[^A_B T^{-1} = ^B_A T = \begin{bmatrix} ^A_B R^T & -^A_B R^T \cdot\ ^AP_{Borg} \\ 0\ 0\ 0 & 1 \end{bmatrix}\]

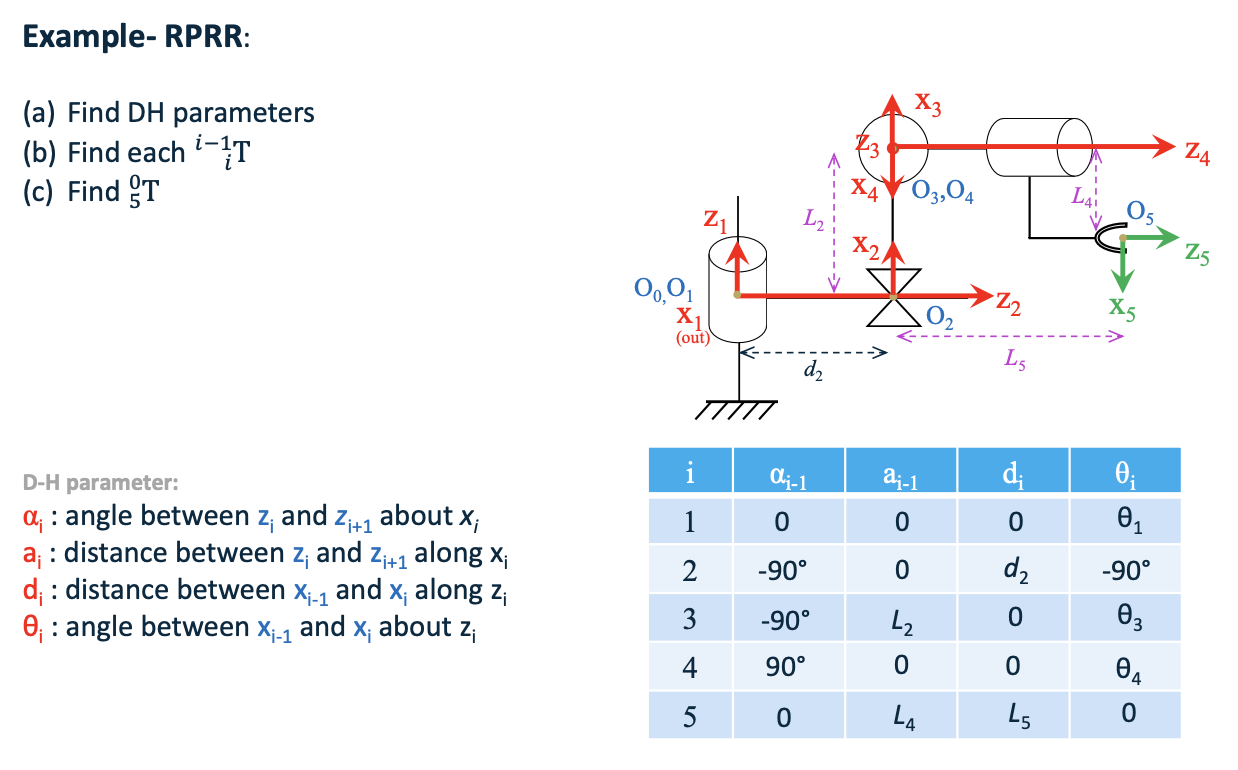
4 alpha a d theta (L5)

右手定则
右手法则是判断旋转角度正负的基础规则：
规则：用右手握住旋转轴，拇指指向轴的正方向（例如，$Z_i$轴的正方向），其余四指的弯曲方向为正旋转方向。
正角度：如果旋转是沿着右手四指弯曲的方向，则角度为正。
负角度：如果旋转是反方向（即与右手四指弯曲方向相反），则角度为负。

$\alpha_{i-1}$：绕$x_{i-1}$轴，从$z_{i-1}$到$z_i$的夹角。

$a_{i-1}$：沿$x_{i-1}$轴，从$z_{i-1}$到$z_i$的距离。(与x垂直)

$d_i$：沿$z_i$轴，从$x_{i-1}$到$x_i$的距离。

$\theta_i$：绕$z_i$轴，从$x_{i-1}$到$x_i$的夹角 (与z垂直)

Forward Kinematics:
$^{i-1}_iT = ^{i-1}_RT\ ^R_QT\ ^Q_PT\ ^P_iT$
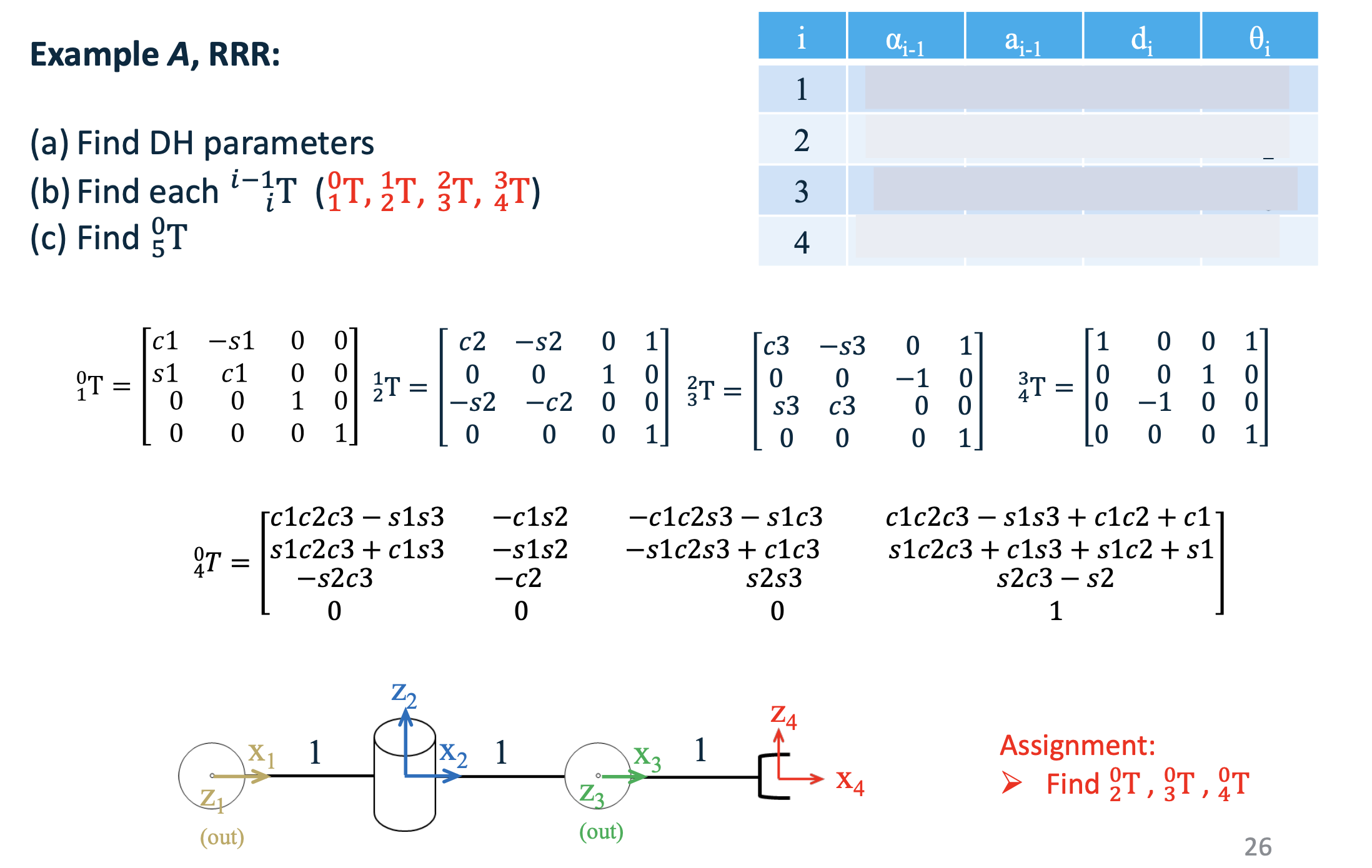
\[{}^{i-1}_i T(\alpha_{i-1}, a_{i-1}, \theta_i, d_i) = R_x(\alpha_{i-1}) D_x(a_{i-1}) R_z(\theta_i) D_z(d_i)\] \[{}^{i-1}_i T = \begin{bmatrix} c\theta_i & -s\theta_i c\alpha_{i-1} & s\theta_i s\alpha_{i-1} & a_{i-1} c\theta_i \\ s\theta_i & c\theta_i c\alpha_{i-1} & -c\theta_i s\alpha_{i-1} & a_{i-1} s\theta_i \\ 0 & s\alpha_{i-1} & c\alpha_{i-1} & d_i \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

eg.1.

eg.2. ？？

eg.3.

eg.4.

模拟题

D = 10cm = 100mm

d = 4cm = 40mm

P = 5MPa

1) $A_1 = \pi \times (D/2)^2 = 7850 mm^2$ $F_{push} = P \times A_1 = 39250 N$ 2) $A_2 = \pi \times(d/2)^2 = 6593mm^2$ $F_{pull} = P\times(A_1-A_2) = 32970N$

1. DOF = 8
2. rongyu = 8 - 6 = 2
0 $90^{\circ}$ 绕轴旋转

import numpy as np

def dh_transform_matrix(a, alpha, theta, d):
    # Convert degrees to radians for trigonometric calculations
    alpha_rad = np.radians(alpha)
    theta_rad = np.radians(theta)
    
    # Construct the transformation matrix
    T = np.array([
        [np.cos(theta_rad), -np.sin(theta_rad) * np.cos(alpha_rad), np.sin(theta_rad) * np.sin(alpha_rad), a * np.cos(theta_rad)],
        [np.sin(theta_rad), np.cos(theta_rad) * np.cos(alpha_rad), -np.cos(theta_rad) * np.sin(alpha_rad), a * np.sin(theta_rad)],
        [0, np.sin(alpha_rad), np.cos(alpha_rad), d],
        [0, 0, 0, 1]
    ])
    
    return T

# Given parameters
a = 0.5
alpha = 90
theta = 30
d = 0.2

# Calculate the matrix
transformation_matrix = dh_transform_matrix(a, alpha, theta, d)

transformation_matrix

  
from sympy import symbols, cos, sin, Matrix, pi, sqrt

def dh_transform_matrix_symbolic(a, alpha, theta, d):
    # Convert degrees to radians
    alpha_rad = alpha * pi / 180
    theta_rad = theta * pi / 180

    # Construct the symbolic transformation matrix
    T = Matrix([
        [cos(theta_rad), -sin(theta_rad) * cos(alpha_rad), sin(theta_rad) * sin(alpha_rad), a * cos(theta_rad)],
        [sin(theta_rad), cos(theta_rad) * cos(alpha_rad), -cos(theta_rad) * sin(alpha_rad), a * sin(theta_rad)],
        [0, sin(alpha_rad), cos(alpha_rad), d],
        [0, 0, 0, 1]
    ])
    return T

# Given parameters
a = 0.5
alpha = 90  # degrees
theta = 30  # degrees
d = 0.2

# Compute the symbolic transformation matrix
transformation_matrix_symbolic = dh_transform_matrix_symbolic(a, alpha, theta, d)

# Display the matrix
transformation_matrix_symbolic